Discrete Math Chapter 8 - Relations

Relations and Their Properties

Binary Relations

Definition: Let A, B be two sets. A binary relation R from A to B is a subset of the Cartesian product $A × B$.

By definition, a binary relation $R ⊆ A × B$ is a set of ordered pairs of the form $(a, b)$ with $a ∈ A$ and $b ∈ B$.

We use a R b to denote $(a, b) ∈ R$, and $a \not R b$ to denote $(a, b) ∉ R$.

Binary Relations vs Functions

Functions can also be visualized as graphs, but they map each element in the domain to exactly one element in the codomain.

Binary relations are able to represent one-to-many relationships between elements in A and B.

Binary relations can be viewed as generalization of functions.

Relations between Finite Sets

Theorem: There are $2^{nm}$ binary relations from an n-element set A to an m-element set B.

Proof:

The cardinality of the Cartesian product $|A × B| = nm$.

R is a binary relation from A to B if and only if $R ⊆ A × B$.

The number of subsets of a set with nm elements is $2^{nm}$.

Matrix representation:

A relation R between finite sets can be represented using a zero–one matrix $M_R$.

$$\left( \begin{matrix} \notag 0&1&0&0&0\\ 1&0&1&1&0\\ 1&0&1&0&1 \end{matrix} \right)$$

Representing Binary Relations

We can visually represent a binary relation R:

as a directed graph: if $a R b$, then draw an arrow from a to b: $a → b$

as a table (matrix): if $a R b$, then mark the table cell at $(a, b)$

Relations on One Set

Definition: A relation on a set A is a relation from A to A.

Properties of Relations

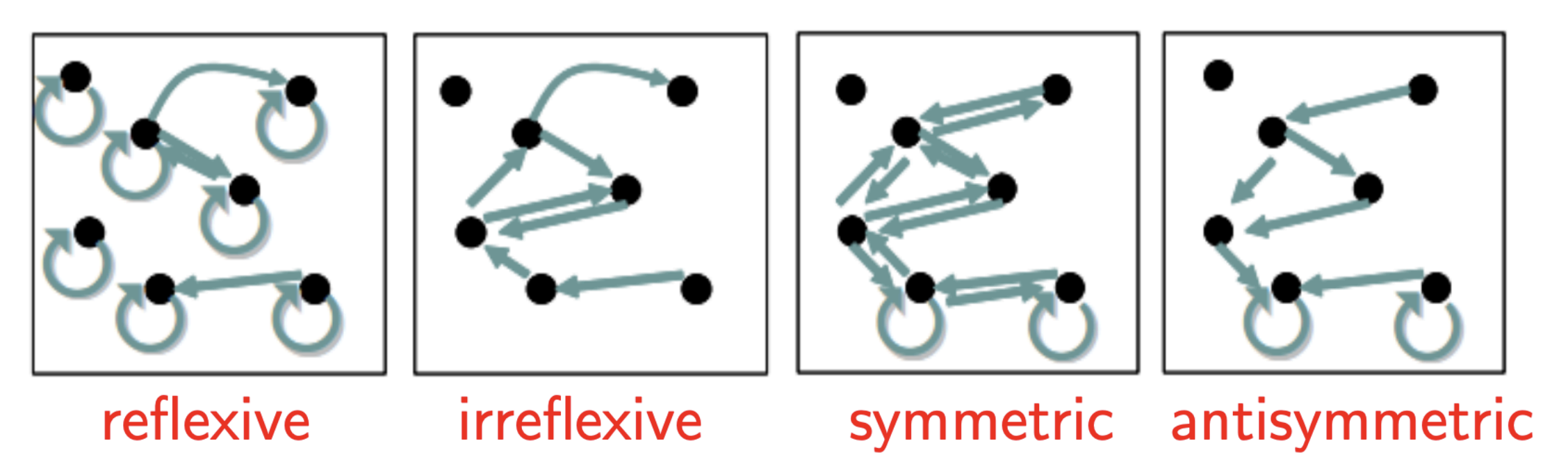
Reflexive Relation(自反):

A relation R on a set A is called reflexive if $(a, a) ∈ R$ for every element $a ∈ A$.

A relation R is reflexive if and only if $M_R$ has 1 in every position on its main diagonal.

Irreflexive Relation(完全非自反):

A relation R on a set A is called irreflexive if $(a, a) ∉ R$ for every element $a ∈ A$.

A relation R is irreflexive if and only if $M_R$ has 0 in every position on its main diagonal.

Symmetric Relation(对称):

A relation R on a set A is called symmetric if $(b, a) ∈ R$ whenever $(a, b) ∈ R$ for all $a, b ∈ A$.

A relation R is symmetric if and only if $M_R$ is symmetric.

Antisymmetric Relation(完全非对称):

A relation R on a set A is called antisymmetric if $(b, a) ∈ R$, $(a, b) ∈ R$ implies $a = b$ for all $a, b ∈ A$.

A relation R is antisymmetric if and only if $m{ij} = 1$ implies $m{ji} = 0$ for $i ≠ j$, where $m_{ij}$ is the (i, j)-th element of $M_R$.

Transitive Relation(传递性):

Transitive Relation: A relation R on a set A is called transitive if $(a, b) ∈ R$, $(b, c) ∈ R$ implies $(a, c) ∈ R$ for all $a, b, c ∈ A$

Combining Relations

Since relations are sets, we can combine relations via set operations: union, intersection, complement, difference, etc. • typically both relations are defined on the same sets

Composite of Relations

Definition: Let R be a relation from a set A to a set B and S be a relation from B to C. The composite of R and S is the relation consisting of the ordered pairs $(a, c)$ where $a ∈ A$ and $c ∈ C$ and for which there exists a $b ∈ B$ such that $(a, b) ∈ R$ and $(b, c) ∈ S$.

We denote the composite of R and S by $S ◦ R$. (先操作的放后面，与函数一致)

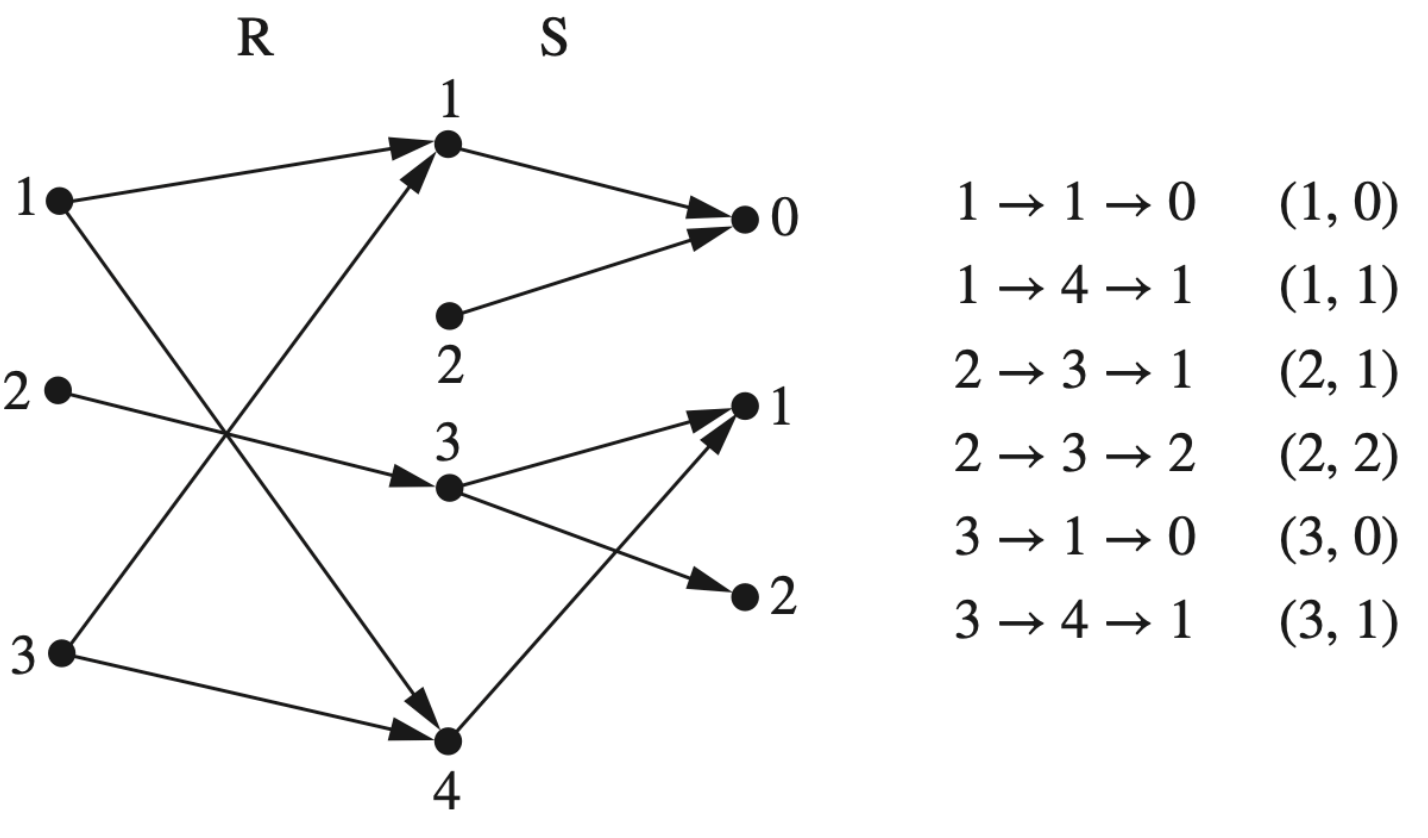
Example : (as a matrix)

$A = {1, 2}, B = {1, 2, 3}, C = {a, b}$

$R = {(1, 2), (1, 3), (2, 1)} ⊆ A × B, S = {(1, a), (3, a), (3, b)} ⊆ B × C$

$S ◦ R = {(1, a), (1, b), (2, a)} $

$$M_R=\left( \begin{matrix} \notag 0&1&1\\ 1&0&0 \end{matrix} \right)$$ $$M_S=\left( \begin{matrix} \notag 1&0\\ 0&0\\ 1&1\end{matrix} \right)$$ $$M_R ⊙ M_S = \left( \begin{matrix} \notag 1&1\\ 1&0\end{matrix} \right)$$

Boolean product ⊙ of matrices: replace + with ∨ and × with ∧

Composing a Relation with Itself

Definition: Let R be a relation on a set A. The powers $R^n$ for $n = 1, 2, 3, …$ is defined inductively by $R^1 = R$ and $R^{n+1} = R^n ◦ R$.

Example: Let A = {1, 2, 3, 4} and R = {(1, 2), (2, 3), (2, 4), (3, 3)}

$$R^1 = R$$ $$R^2 = R ◦ R = {(1, 3), (1, 4), (2, 3), (3, 3)}$$ $$R^3 = R^2 ◦ R = {(1, 3), (2, 3), (3, 3)}$$ $$R^4 = R^3 ◦ R = {(1, 3), (2, 3), (3, 3)}$$ $$R^k = R^4 = …$$

Transitive Relation and $R^n$

Theorem: The relation R on a set A is transitive if and only if

$$R^n ⊆ R\ for\ n = 1, 2, 3, …$$

Note that Rn can be computed by Boolean product of matrices:

$$M_{R^n} = M_R ⊙ M_R ⊙ ··· ⊙ M_R$$

N-ary Relations and Databases

N-ary Relations

Definition: An n-ary relation R on sets $A_1, A_2, …, A_n$, written as $R : A_1, …, A_n$, is a subset of $A_1 × ··· × A_n$ (Cartisian product of n elements).

The sets Ai s are called the domains of R.

The degree of R is n.

R is functional in domain Ai if for any ai ∈ Ai the relation R contains at most one n-tuple of the form $(···, a_i, ···)$. * R can be indexed by $a_i$

Some ways to represent n-ary relations:

as an explicit list or table of its tuples

as a function from the domains to ${T, F}$

Relational Databases

A relational database is essentially an n-ary relation R.

A domain $A_i$ is a primary key for the database if the relation R is functional in $A_i$. * because R can be indexed by $a_i$

A composite key for the relational database is a set of domains ${···, Ai, ···, Aj, ···}$ such that R contains at most one n-tuple of the form $(···, a_i, ···, a_j, ···)$ for each composite value $(a_i, a_j) ∈ A_i × A_j$ .

R can be indexed by $(a_i, a_j)$

Operations on Databases

Selection Operators

Let A be an n-ary domain $A = A_1 × ··· × A_n$, and let $C : A → {T, F}$ be any condition (predicate) on elements (n-tuples) of A.

The selection operator $s_C$ is the operator that maps any n-ary relation R on A to the n-ary relation consisting of all n-tuples from R that satisfy C. * note that sC(A) is also an n-ary relation

$$∀R ⊆ A, s_C(R) = R ∩ \{a ∈ A | C(a) = T\} = \{a ∈ R | C(a) = T\}$$

Example: Consider $A = StudentName\ ×\ Standing\ ×\ SIDs$

Condition $UpperLevel(name,\ standing,\ sid)$ is defined as $(standing\ =\ junior )\ ∨\ (standing\ =\ senior)$

Then, sUpperLevel is the selection operator that takes any relation R on A (database of all students) and produces a relation $R’ ⊆ R$ consisting of just the upper-level students (juniors or seniors).

Projection Operators

Let A be an n-ary domain $A = A_1 × ··· × A_n$, and let ${i_1, …, i_m}$ be a sequence of indices such that $1 ≤ i_1 < ··· < i_m ≤ n$ and $m < n$.

The projection operator $P{i1, …, i_m} : A → A{i1} × ··· × A{i_m}$ is the operator that maps any n-ary relation R on A to the m-ary relation consisting of m-tuples specified by indices

$${i_1, …, i_m}: P{i_1, …, i_m } (a_1, …, a_n) = (a_{i_1} , …, a_{i_m} )$$

Example: Consider $Cars = Model × Year × Color$

Index sequence is {1, 3}.

The projection operator $P${1, 3} simply maps each 3-tuple, e.g., $(a1, a2, a3) = (Tesla, 2020, black)$ to $(a1, a3) = (Tesla, black)$.

This operator can be applied to any relation $R ⊆ Cars$ to obtain a list of model-color combinations available.

Join Operators

The join operator puts two relations together to form a sort of combined relation.

If the tuple $(a, b)$ appears in $R_1 ⊆ A × B$, and the tuple $(b, c)$ appears in $R_2 ⊆ B × C$, then the tuple $(a, b, c)$ appears in their join $J(R_1, R_2)$.

In general, A, B, C can each be the Cartesian product of multiple domains rather than a single domain.

Example: Let relation $R_1$ be a teaching assignment table, relating Professors to Courses.

Let relation $R_2$ be a classroom assignment table, relating Courses to Rooms and Times.

Then, the relation $J(R_1, R_2)$ is like your class schedule, listing tuples of the form (professor, course, room, time).

Closures of Relations(闭包)

Definition: Let R be a relation on a set A. A relation S on A with property P is called the closure of R with respect to P if S is the minimal set containing R satisfying the property P.

Minimal S: for every relation Q ⊇ R that satisfies P, we have S ⊆ Q.

Reflexive Closures

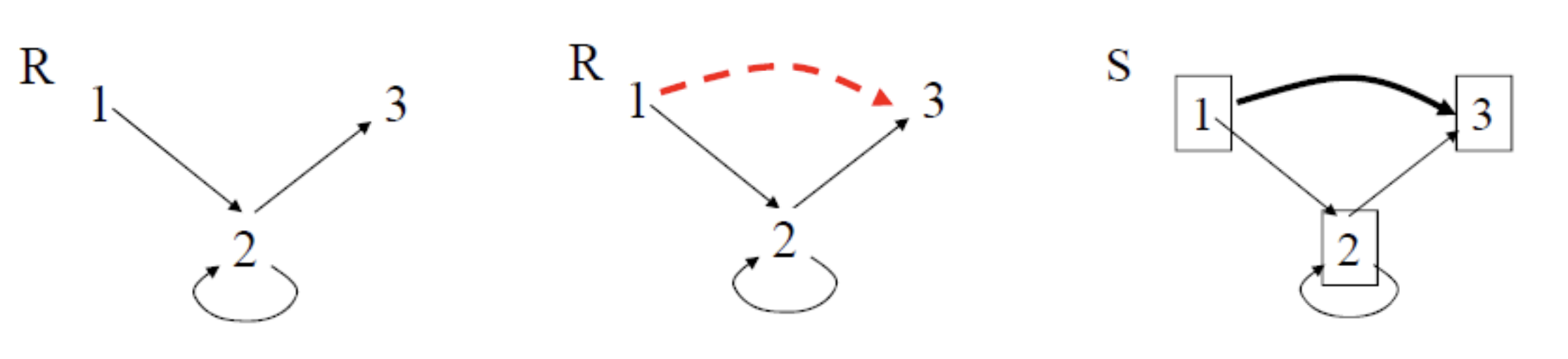
Consider R = {(1, 1), (1, 2), (2, 1), (3, 2)} defined on A = {1, 2, 3}.

Q: Is relation R reflexive?

No, (2, 2) and (3, 3) are not in R What is the minimal re lation S ⊇ R that is reflexive?

How to make R reflexive by adding minimum number of pairs?

Add (2, 2) and (3, 3): S = {(1, 1), (1, 2), (2, 1), (3, 2), (2, 2), (3, 3)} ⊇ R is reflexive.

Symmetric Closures

symmetric closure: relation R = {(1, 2), (1, 3), (2, 2)} on A = {1, 2, 3}

how to make it symmetric?

S = {(1, 2), (1, 3), (2, 2)} ∪ {(2, 1), (3, 1)}

General solution:

$$R \cup R^{-1}$$

Paths and Transitive Closures

Definition: A (directed) path from a to b in a directed graph G is a sequence of edges $(x0, x1), (x1, x2), …, (xn−1, xn)$ in graph G, where $n ≥ 0, x_0 = a$ and $x_n = b$.

Recall that we can represent a relation using a directed graph.

Then, finding a transitive closure corresponds to finding B of elements that are connected with a directed path.

Example: Relation R = {(1, 2), (2, 2), (2, 3)} on A = {1, 2, 3}

The transitive closure of R is S = {(1, 2), (2, 2), (2, 3), (1, 3)}

Paths and Powers of a Relation

Theorem: Let R be relation on a set A. There is a path of length n from a to b in R (as a directed graph) if and only if $(a, b) ∈ R_n$.

The Connectivity Relation R*

Definition: R is a relation on a set A. The connectivity relation $R^∗$ consists of all pairs (a, b) such that there is a path (of any length) from a to b in R.

$$R^*=\cup^\infty_{k=1}R^k$$

Example: Relation R on A = {1, 2, 3, 4} shown in the figure below

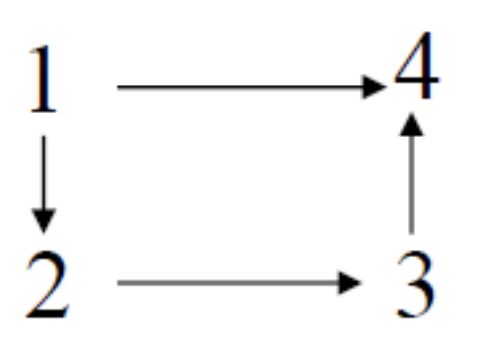
$R$ = {(1, 2), (1, 4), (2, 3), (3, 4)}

$R^2$ ={(1, 3), (2, 4)}

$R^3$ ={(1, 4)}

$R^4$ = ∅

$R^∗$ = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}

Theorem: The transitive closure of a relation $R$ equals the connectivity relation $R^∗$.

Finding Transitive Closures

Recall that finding a transitive closure corresponds to finding the connectivity relation, which consists of all pairs of elements that are connected with a directed path.

Lemma: Let A be a set with n elements and R be a relation on A. If there is a path in R from a to b, then there is such a path with length ≤ n. Moreover, when a ≠ b, if there is a path from a to b, then there is such a path with length ≤ n − 1. That is,

$$R^*=\cup^n_{k=1}R^k$$

Theorem: Let $M_R$ be the zero–one matrix of the relation R on a set with n elements. Then the zero–one matrix of the transitive closure R is

$$M_{R^*}=M_R \vee M_R^{[2]}\vee M_R^{[3]}\vee M_R^{[4]}\vee ...\vee M_R^{[n]}$$ $$M_R^{[n]}=M_R ⊙M_R⊙...=M_{R^n}$$

Naive algorithm

The Floyd-Warshall algorithm:

By definition, $R^∗$ consists of all pairs (a, b) such that there exists a path from a to b in the graph representation of R.

This algorithm computes by iterating on k: in the k-th iteration, the intermediate nodes of all paths are from the first k nodes only.

Equivalence Relations

Definition: A relation R on a set S is called an equivalence relation if it is reflexive, symmetric, and transitive.

Equivalence Classes

Definition: Let R be an equivalence relation on a set S. The set of all elements that are related to an element a of S is called the equivalence class of a, denoted by $[a]_R$. When only one relation is considered, we use the notation $[a]$.

$$[a]_R=\{b \in S:(a,b)\in R\}$$

Example:

$R = {(a, b) : a ≡ b mod 3}$ on S = {0, 1, 2, 3, 4, 5, 6}

[0] = [3] = [6] = {0, 3, 6}

[1] = [4] = {1, 4}

[2] = [5] = {2, 5}

Find [a] for the following relations:

“Strings a and b have the same length.”

$$[a] = the\ set\ of\ all\ strings\ of\ the\ same\ length\ as\ string\ a$$

“Integers a and b have the same absolute value.”

$$[a] = \{a, −a\}$$

“Real numbers a and b have the same fractional part: $a − b ∈ Z$.”

$$[a] = \{..., a − 2, a − 1, a, a + 1, a + 2, ...\}$$

Theorem:

Let R be an equivalence relation on a set S. The following statements are equivalent:

(i) $a R b $

(ii) $[a] = [b]$

(iii) $[a] ∩ [b] ≠ ∅$

Partition of a Set S

Definition: Let S be a set. A collection of nonempty subsets of S $A_1, A_2, …, A_k$ is called a partition of S if:

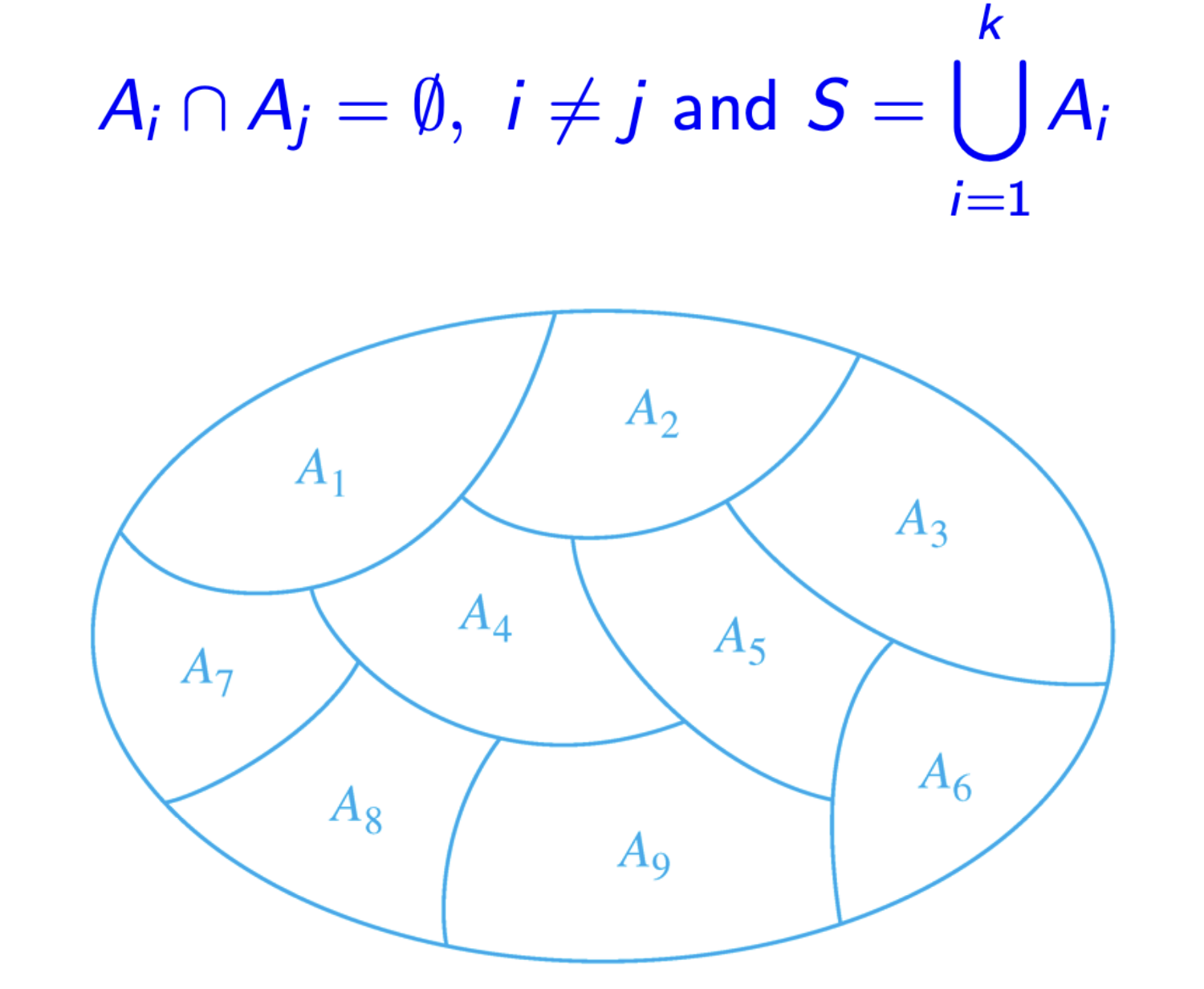
Theorem: Let R be an equivalence relation on a set S. Then the union of all the equivalence classes of R is S:

$$S=\cup_{a \in S}[a]_R$$

Theorem: The equivalence classes form a partition of S.

Theorem: Let {A1, A2, …, Ai, …} be a partition of S. Then there is an equivalence relation R on S, which has the sets Ai as its equivalence classes.

Partial Orderings

Definition: A relation R on a set S is called a partial ordering, or partial order, if it is reflexive, antisymmetric, and transitive.

A set S together with a partial ordering R is called a partially ordered set, or poset, denoted by (S, R) or simply (S, ≼) in general. Members of S are called elements of the poset.

Notation: The notation $a ≺ b$ denotes that $a ≼ b$ but $a ≠ b$. Also, we say “a is less than b” or “b is greater than a” if $a ≺ b$

Comparability

Definition: The elements a, b of a poset (S, ≼) are comparable if $a ≼ b$ or $b ≼ a$. Otherwise, a and b are called incomparable.

If a, b has partial ordering relations, a,b and b, a are comparable.

Example: S = {1, 2, 3, 4, 5}, R denotes the “ | ” relation

Is 2, 4 comparable? Yes

Is 5, 5 comparable? Yes

Is 3, 5 comparable? No, because neither of 3 | 5 and 5 | 3 holds

Total Ordering

Definition: If (S, ≼) is a poset and every two elements of S are comparable, then ≼ is called a total order or linear order.

S is called a totally ordered or linearly ordered set. A totally ordered set is also called a chain.

Example: Consider S = {1, 2, 3, 4, 5}

Is (S , ≥) a totally (linearly) ordered set? Yes

Is (S , | ) a totally (linearly) ordered set? No, because 3, 5 are not comparable

Cover

Definition: If (S, ≼) is a poset, $\forall x,y \in S$, $x\leq y, x\neq y$, there is no $x\leq z \leq y$

y cover x, y is 前驱， x is 后继

$Cover(A)={(x,y)|x,y \in A , y\ cover\ x}$

Example: Consider S={1,2,4,6}

poset is (A,|)

$Cover(A)= (1,2),(2,4),(2,6)$ without (1,4) because 1|2|4

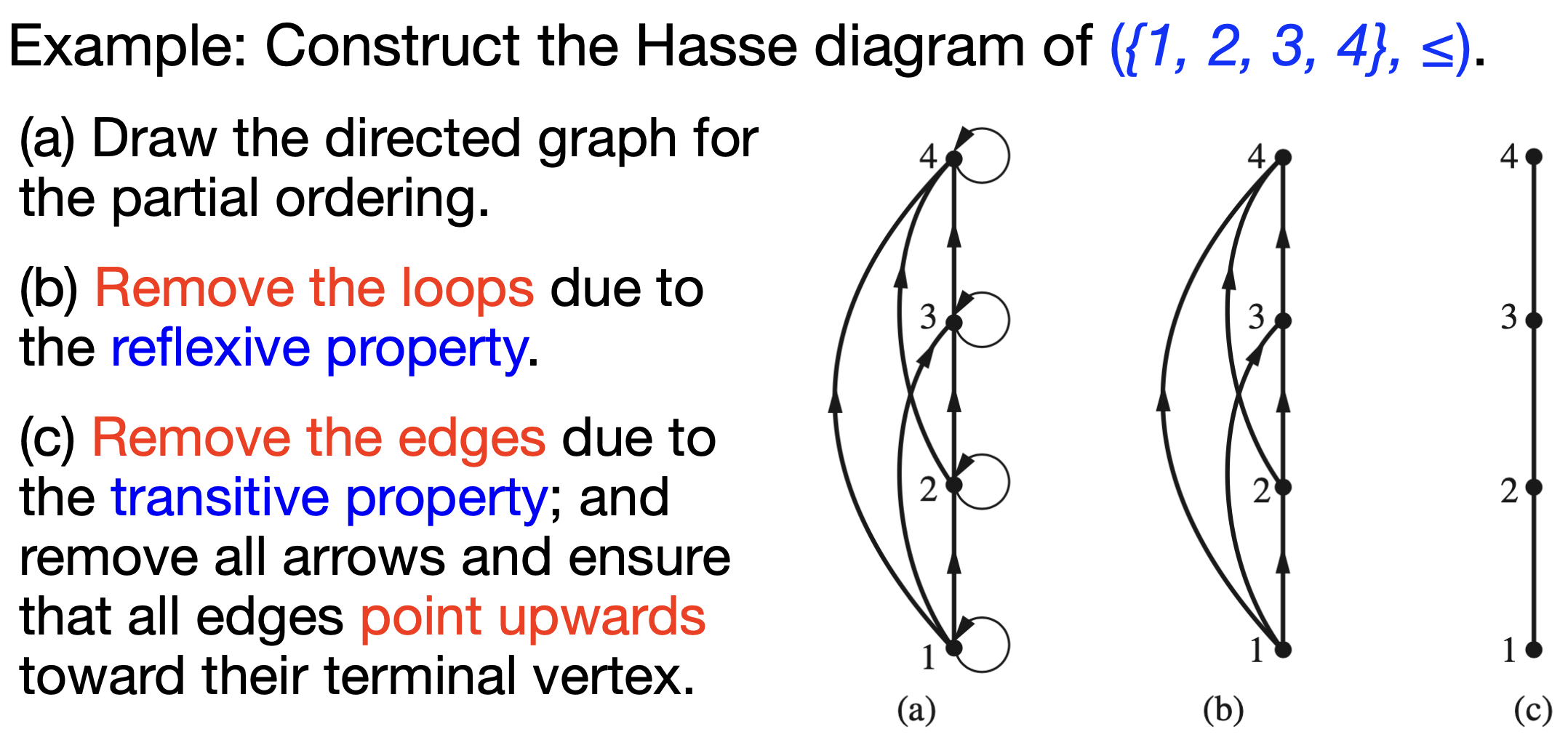
Hasse Diagram

cover图，无环，无第三边，无双边

1. if $x\leq y$, then x under y
2. if y covers x, connect x and y

Reflexive, transitive

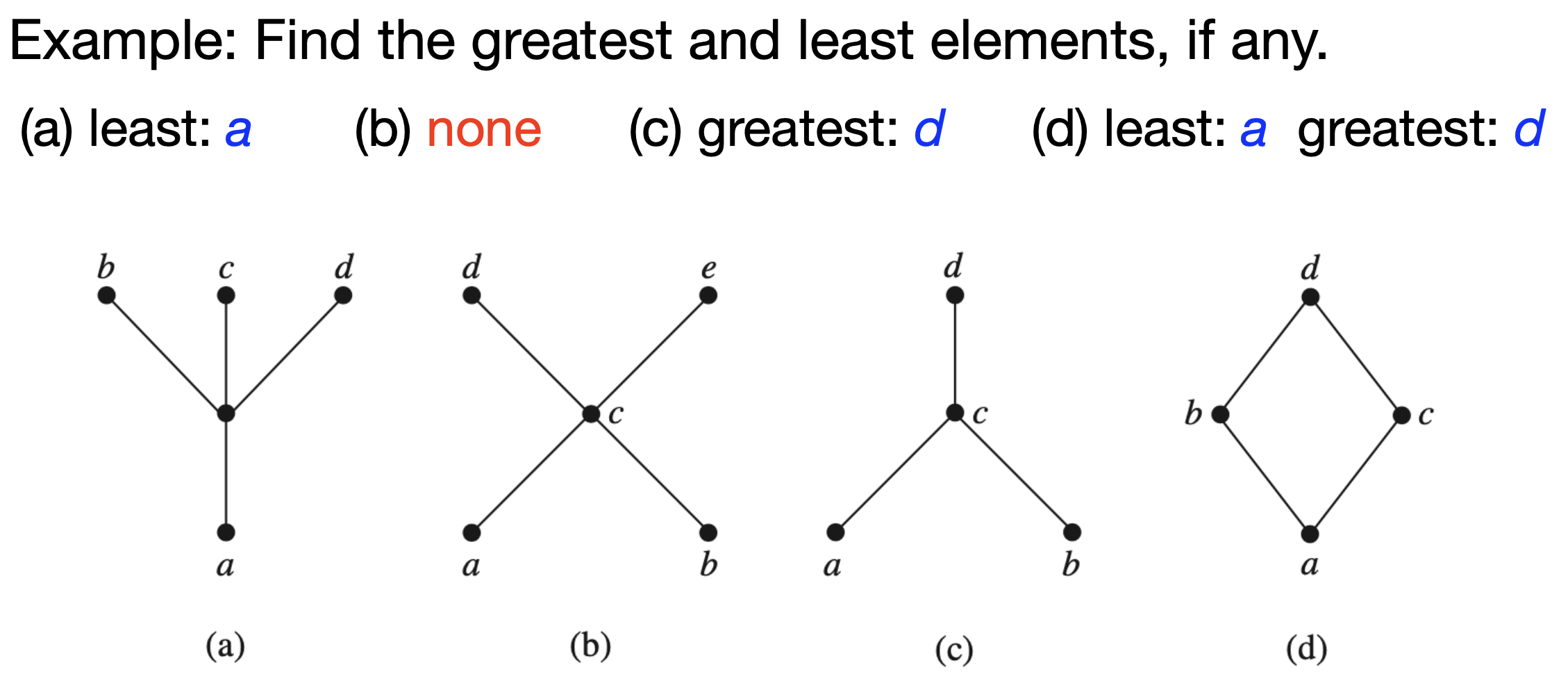
Maximal and Minimal Elements(极大元，极小元)

Definition: a is a maximal (resp. minimal) element in poset $(S, ≼)$ if there is no $b ∈ S$ such that $a ≺ b$ (resp. $b ≺ a$).

Example: consider the poset ({2, 4, 5, 10, 12, 20, 25}, | )

What are the maximal elements? 12, 20, 25

What are the minimal elements? 2, 5

极大元之间不可比

Greatest and Least Elements(最大元，最小元)

Definition: a is the greatest (resp. least) element of poset $(S, ≼)$ if $b ≼ a$ (resp. $a ≼ b$) for all $b ∈ S$.

Upper and Lower Bounds

Definition: Let A be a subset of a poset $(S, ≼)$.

$u ∈ S$ is called an upper bound (resp. lower bound) of A if $a ≼ u$ (resp. $u ≼ a$) for all $a ∈ A$.

$x ∈ S$ is called the least upper bound (resp. greatest lower bound) of A if x is an upper bound (resp. lower bound) that is less than any other upper bound (resp. lower bound) of A.

Example: Find the greatest lower bound and the least upper bound of set {1, 2, 4, 5, 10}, if they exist, in the poset ( Z+ , | ).

greatest lower bound(下确界): 1

least upper bound(上确界): 20

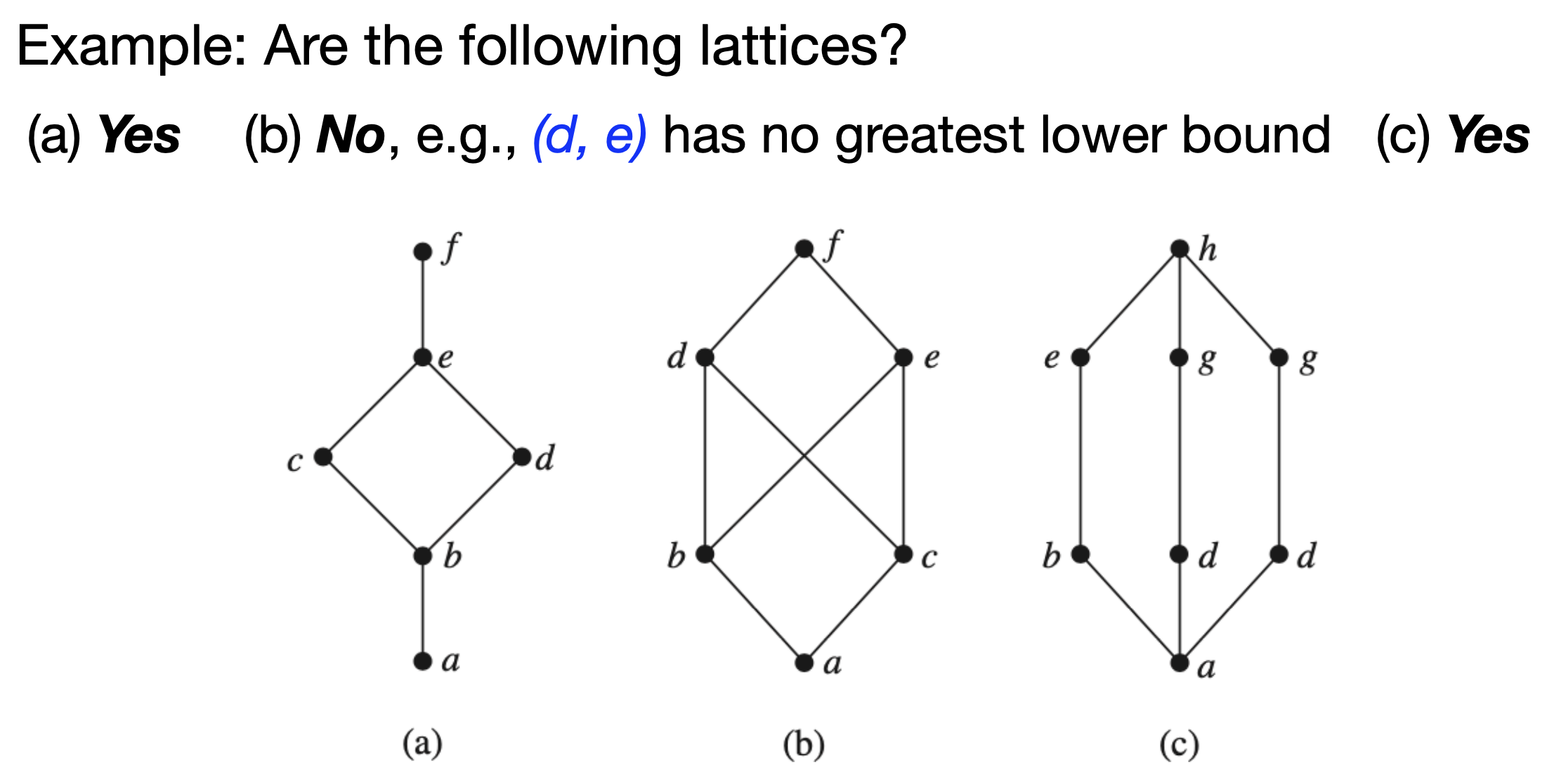
Lattices

Definition: A partially ordered set in which every pair of elements has both a least upper bound and a greatest lower bound is called a lattice.

Well-Ordered Induction

Definition: $(S, ≼)$ is a well-ordered set if $≼$ is a total order and every nonempty subset of S has a least element.

The principle of well-ordered induction: Suppose that S is a well-ordered set.

To prove that $P(x)$ is true for all $x ∈ S$, we complete two steps:

Basis step: prove $P(x_0)$ is true for the least element $x_0$ of S

Inductive step: prove, for every $y ∈ S$, if $P(x)$ is true for all $x ∈ S$ with $x ≺ y$, then $P(y)$ is true.

Proof by contradiction: consider the set {$x ∈ S : P(x)$ is false}.

Topological Sorting

Given a partial ordering R, a total ordering ≼ is said to be compatible with R if a ≼ b whenever a R b.

Topological sorting: construct a compatible total ordering from a partial ordering.

Theorem: Every finite nonempty poset $(S, ≼)$ has at least one minimal element.

Exercise

1. Let $A = $ {a, b, c} and $B = $ {1, 2, 3}

Is $R = {(a, 1), (b, 2), (c, 2)}$ a relation from A to B?

Yes

Is $Q = {(1, a), (2, b)}$ a relation from A to B?

No, it’s a relation from B to A

Is $P = {(a, a), (b, c), (b, a)}$ a relation from A to A?

Yes

2. Consider relations on A = {1, 2, 3, 4}

Is $R_{div} = {(a, b) : a | b}$ transitive?

Yes, because if $a | b$ and $b | c$ then $a | c$

Is $R_≠ = {(a, b) : a ≠ b}$ transitive?

No, because $(1, 2), (2, 1) ∈ R≠$ but $(1, 1) ∉ R≠$

Is $R = {(1, 2), (2, 2), (3, 3)}$ transitive?

Yes

3. Consider binary relations on a finite set A with |A| = n:

Hint: think of a binary relation as a zero-one matrix

How many reflexive relations?

$$2^{n^2-n}$$

How many irreflexive relations?

$$2^{n^2-n}$$

How many symmetric relations?

$$2^{(n^2+n)/2}$$

How many antisymmetric relations?

$$2^n \cdot 3^{(n^2-n)/2}$$

Diagonal has $n$ possible cases, either 0/1; each slot beside diagonal elements can be either$(0,0),(0,1)$ or $(1,1)$

4. Prove that “If R is transitive, then Rn is also transitive.”

Let $P(n)$ be the theorem statement

Basic step: $n=1$ : The statement is trivially true.

Inductive step: Assume $P(k)$ is true for an arbitrary integer $k \geq 1$, we need to show that $P(k + 1)$ is true. By the previous Theorem, $P(k + 1)$ means: for any path $p(a, b)$ of length k + 1 from a to b and any path $p(b, c)$ of length k + 1 from b to c, our goal is to find a path $p(a, c)$ from a to c of length k + 1.

Let $p(a, b) = (a, x) + (x, y) + p(y, b)$, then $p(y, b)$ is of length k – 1 ≥ 0. Since R is transitive, $(a, x), (x, y) ∈ R$ implies that $(a, y) ∈ R$. So, $(a, y) + p(y, b)$ is a path from a to b of length 1 + k – 1 = k.

Let $p(b, c) = p(b, z) + (z, c)$, then $p(b, z)$ is also of length k. By the inductive hypothesis, we can find a path $p(a, z)$ from a to z of length k. So, $p(a, z) + (z, c)$ is a path from a to c of length k + 1.

5. For the relation R shown in the figure, find the Floyd-Warshall matrices $W_1, W_2, W_3, W_4$.

(Here $W_k$ is the matrix after the k-th iteration and $W_4$ is the transitive closure of R.)

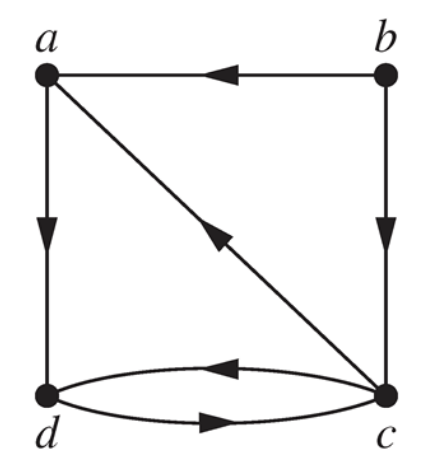
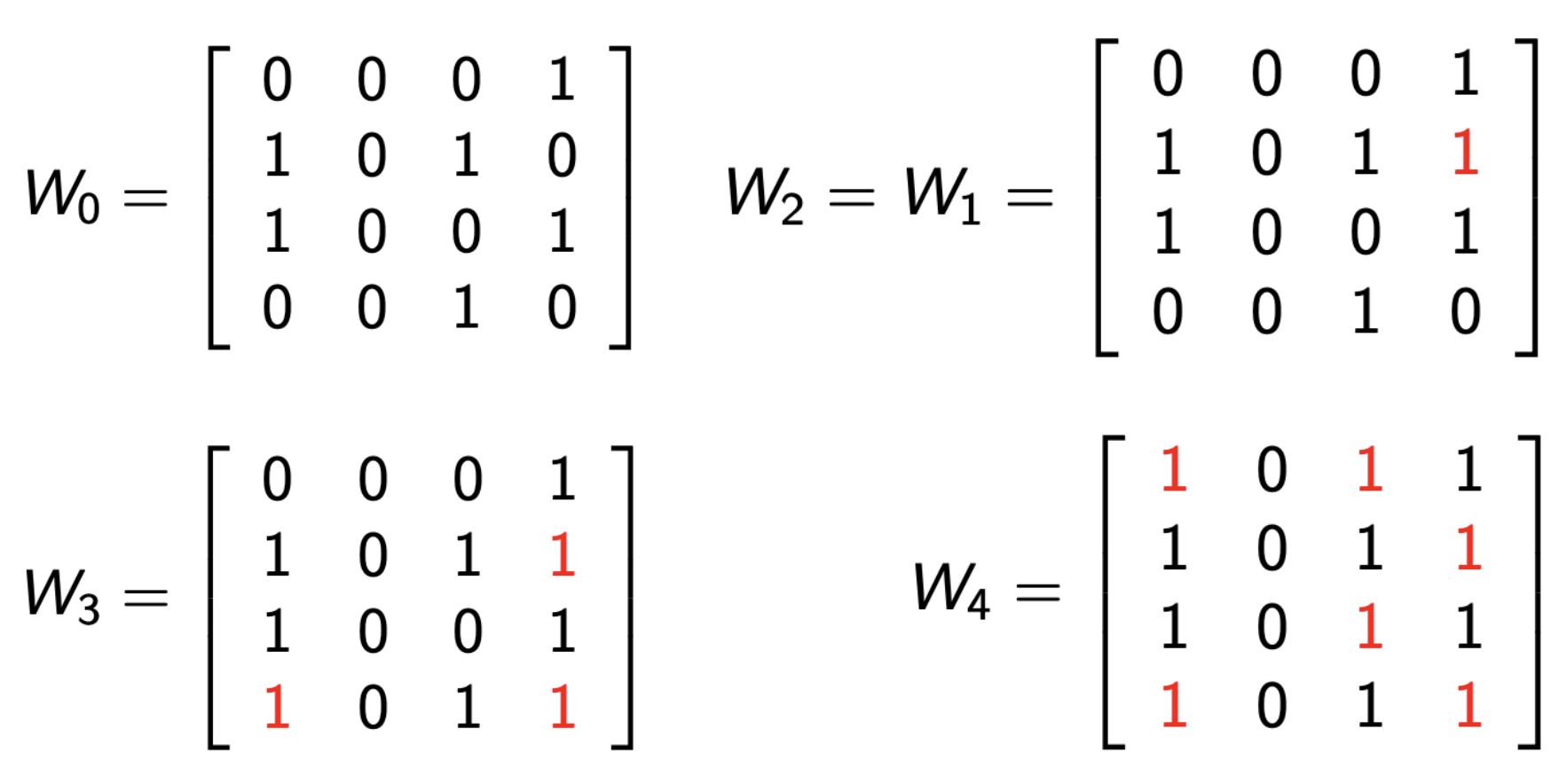
6. Are the following relations equivalence relations?

“Integers a and b have the same absolute value.” Yes

“The relation ≥ between real numbers.” No, not symmetric

“Real numbers a and b have the same fractional part: $a − b ∈ Z$.” Yes

“Natural numbers have a common factor > 1.” No, not reflexive, e.g., (1, 1) ∉ R