DSAA Tree Review

Tree

Basic Concepts

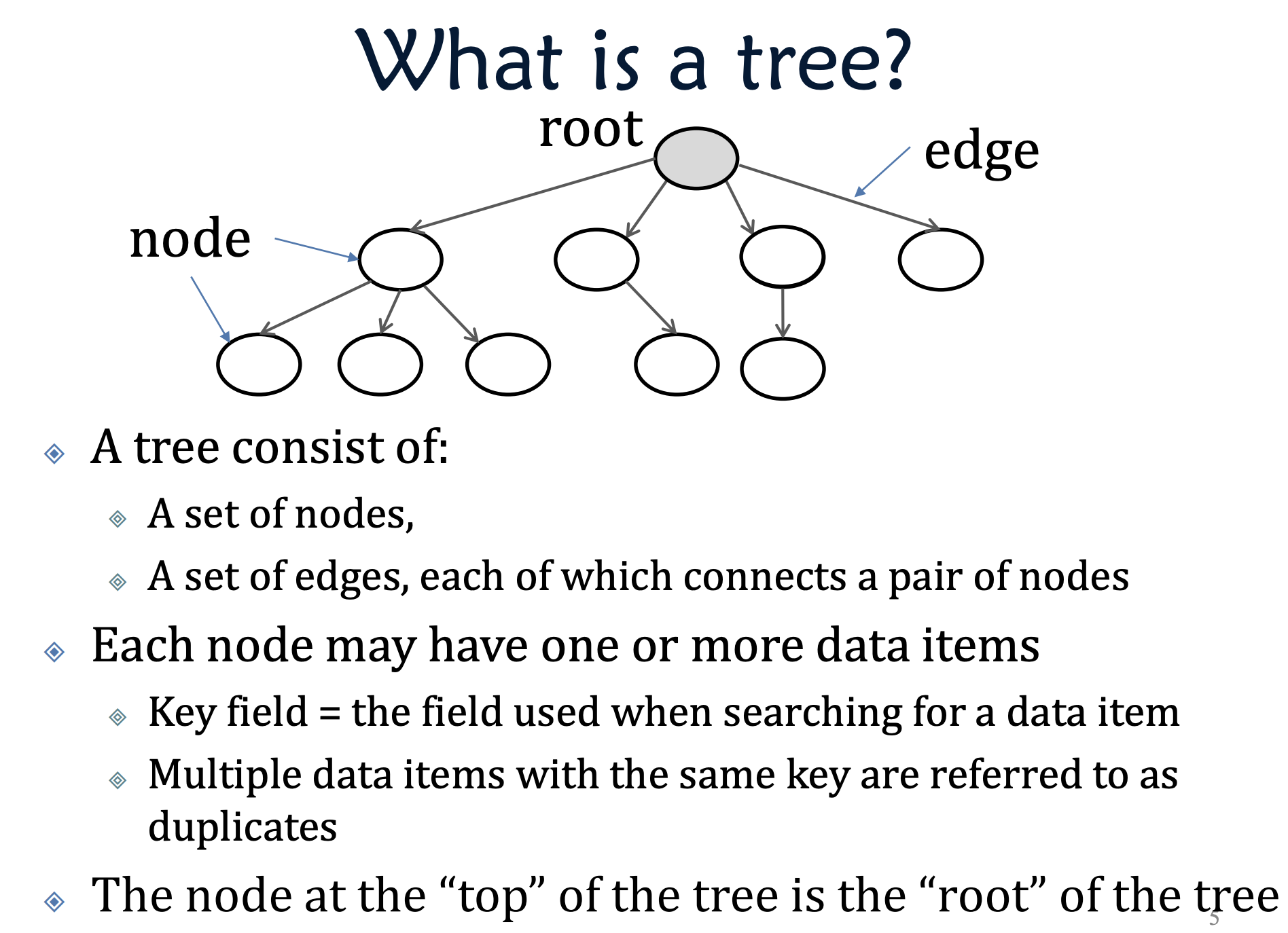
Properties of Tree(binary tree)

1. A tree with n nodes with n-1 edges.

Prove: Every node is pointed at by an edge except for the root.

2. Let T be a tree where every internal node has at least 2 child nodes. If m is the number of leaf nodes, then the number of internal nodes is at most m-1.

Prove: Let n denote the total number of nodes in the tree.

$$n=i+m$$

Where i is the number of internal nodes, m is the number of leaf nodes.

A tree has n-1 edges.

Each internal nodes contributes at least 2 edges. Let the total numbet of edges connected to internal nodes be $2i$. However, note that $i-1$ of these edges are internal connections.

$$n-1 = i+m-1$$ $$2i\leq i+m -1 \longrightarrow i\leq m-1$$

3. A complete binary tree with n ≥ 2 nodes has height O(log n)

Prove: In the k-th level, there can be at most $2^k$ nodes.

The total number of nodes in a complete binary tree of height h is

$$1+2+4+...+2^h=2^{h+1}-1$$ $$2^h\leq n \leq2^{h+1}-1$$ $$h\leq log_2n \leq h+1 \longrightarrow h=\lfloor log_2n\rfloor$$ $$h \in O(log\ n)$$

Binary Tree Traversal

Preorder Traversal

preorderprint(treeNode root):
1. print(root)
2. if(root->left!=null)
3. preorderprint(root->left)
4. if(root->right!=null)
5. preorderprint(root->right)

Inorder Traversal

inorderprint(treeNode root):
1. if(root->left!=null)
2. inorderprint(root->left)
3. print(root)
4. if(root->right!=null)
5. inorderprint(root->right)

Postorder Traversal

postorderprint(treeNode root):
1. if(root->left!=null)
2. postorderprint(root->left)
3. if(root->right!=null)
4. postorderprint(root->right)
5. print(root)

Level Traversal

levelprint(treeNode root):
1. queue cur = new queue
2. root.inqueue();
3. treeNode cur = root;
4. while(!cur.isEmpty()){
5. cur.children.inqueue;
6. cur.dequeue;

Binary Tree applications

Algebraic expression

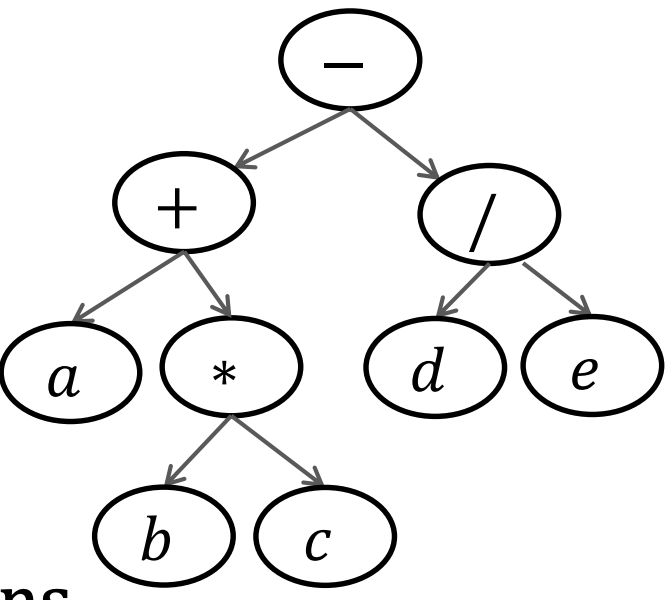
Inorder gives conventional algebraic notation

print “(” before visit left tree

print “)” after visit right tree

for tree at right: ((a+(b*c))-(d/e))

Preorder gives functional notations

Print “(” and “)” as for inorder, and commas after visit left subtree

for tree above: subtr(add(a,mult(b,c)),divide(d,e))

Postorder gives the order in which the computation must be carried out on a stack.

for tree above: push a, push b, push c, multiply, add, …

Huffman encoding

Huffman encoding is a type of variable-length encoding that is based on the actual character frequencies in a given document.

Huffman encoding uses a binary tree:

to determine the encoding of each character

to decode an encoded file

Example:

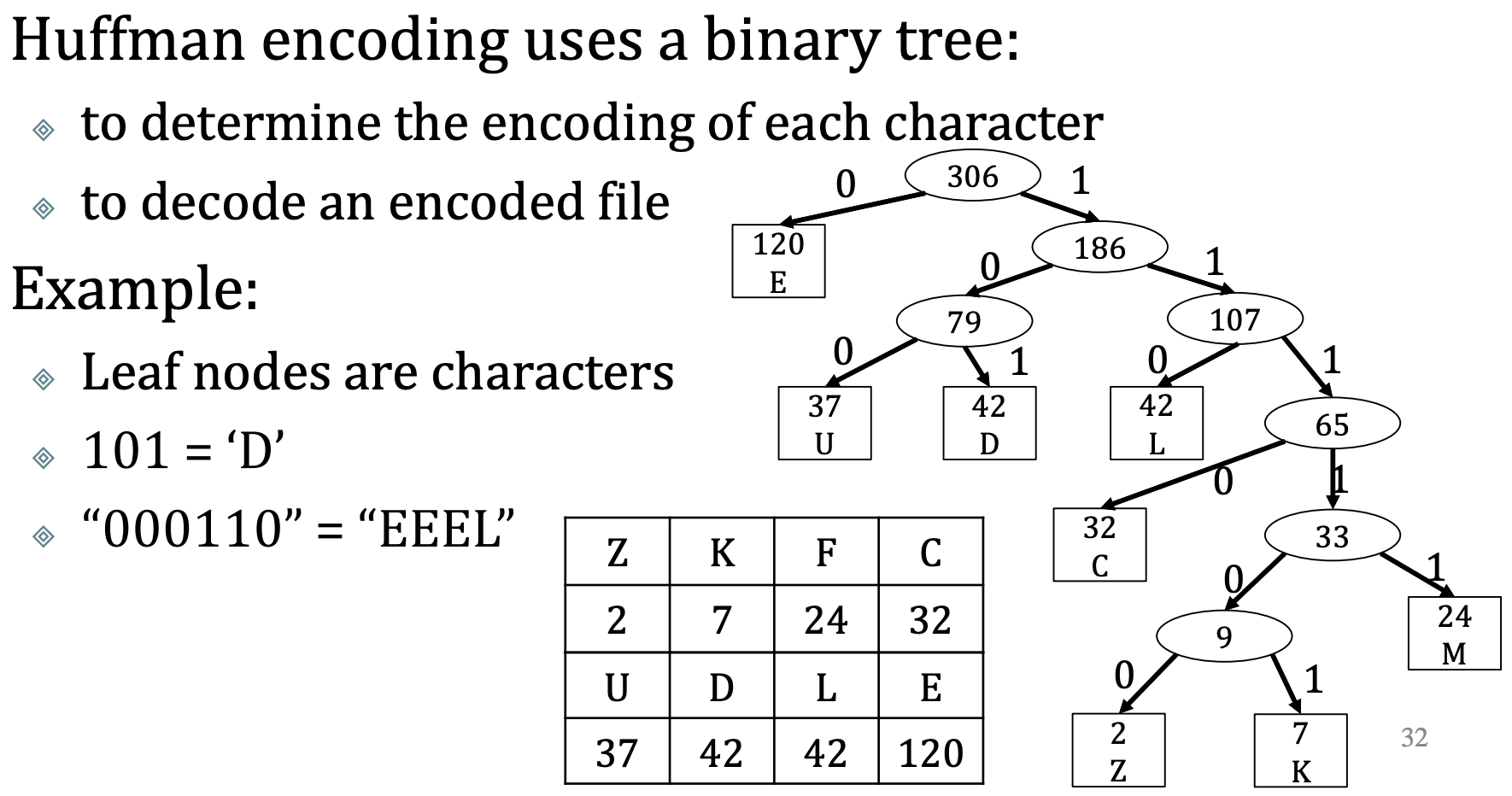
Leaf nodes are characters

101 = ‘D’

“000110” = “EEEL”

Construction

Begin by reading through the text to determine the frequencies

Create a list of nodes that contain (character, frequency) pairs for each character that appears in text

Remove and “merge” the nodes with the two lowest frequencies, forming a new node that is their parent

Add the parent to the list of nodes

Repeat steps 3) and 4) until there is only a single node in the list, which will be the root of the Huffman tree.

Correctness

Given a Huffman tree, it includes at least 2 nodes, assume node u and node v have the top-2 lowest frequencies, then

node u and v have the same parent node

depth(u) and depth(v) >= depth(x), where node x is any leaf node in the Huffman tree.

Huffman encoding is the optimum prefix code, i.e., the space cost is minimized.

Priority Queue

Definition

We will implement a priority queue using a data structure called the “binary heap” to achieve the following guarantees:

O(n) space consumption

O(log n) insertion time

O(log n) delete-min time

The binary heap data structure is an array object that we can view as a complete binary tree.

Level 0 to h-1 are full

Leaf nodes in level h are “as far left as possible”

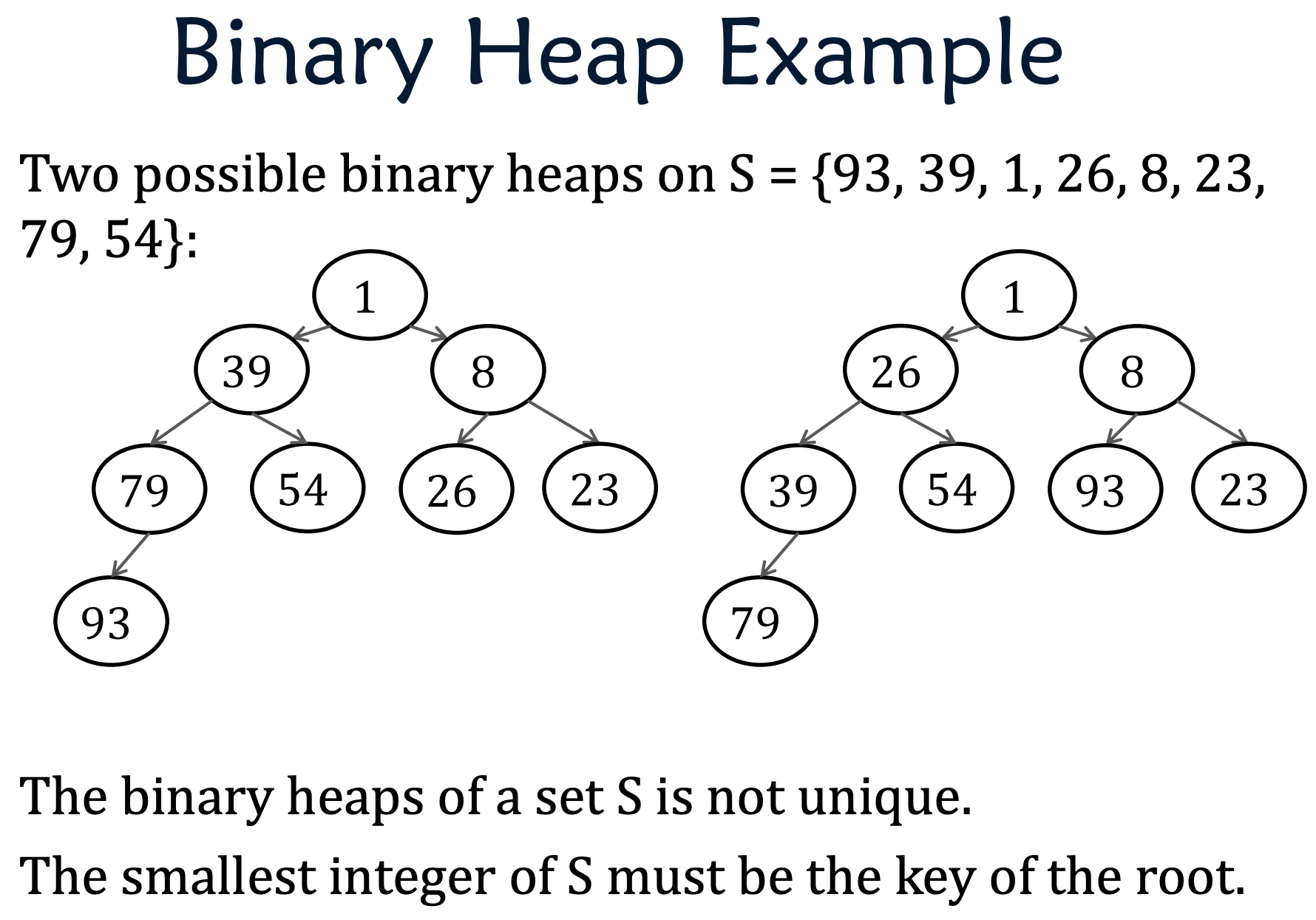
Let S be a set of n integers. A binary heap on S is a binary tree T satisfying:

(1) T is complete

(2) Every node u in T corresponds to a distinct integer in S, the integer is called the key of u (and is stored at u)

(3) If u is an internal node, the key of u is smaller than those of its child nodes

Note that:

Condition 2 implies that T has n nodes.

Condition 3 implies that the key of u is the smallest in the subtree of u.

Insertion / delete-min

Binary Heap Insertion

We perform insert(e) on a binary heap T as follows:

Step 1: Create a leaf node z with key e, while ensuring that T is a complete binary tree, it means there is only one place where z could be added.

Step 2: Set u <-z

Step 3: If u is the root, return.

Step 4: If the key of u > the key of its parent p, return

Step 5: Otherwise, swap the keys of u and p. Set u <- p, and repeat from Step 3.

Binary Heap Delete-min

We perform delete-min on a binary heap T as follows:

Step 1: Report the key of the root

Step 2: Identify the rightmost leaf z at the bottom level of T

Step 3: Delete z, and store the key of z at the root

Step 4: Set u <- the root

Step 5: If u is leaf, return

Step 6: If the key of u < the keys of the children of u, return

Step 7: Otherwise, let v be the child of u with a smaller key. Swap the keys of u and v. Set u <-v, and repeat from Step 5

Find Rightmost Leaf

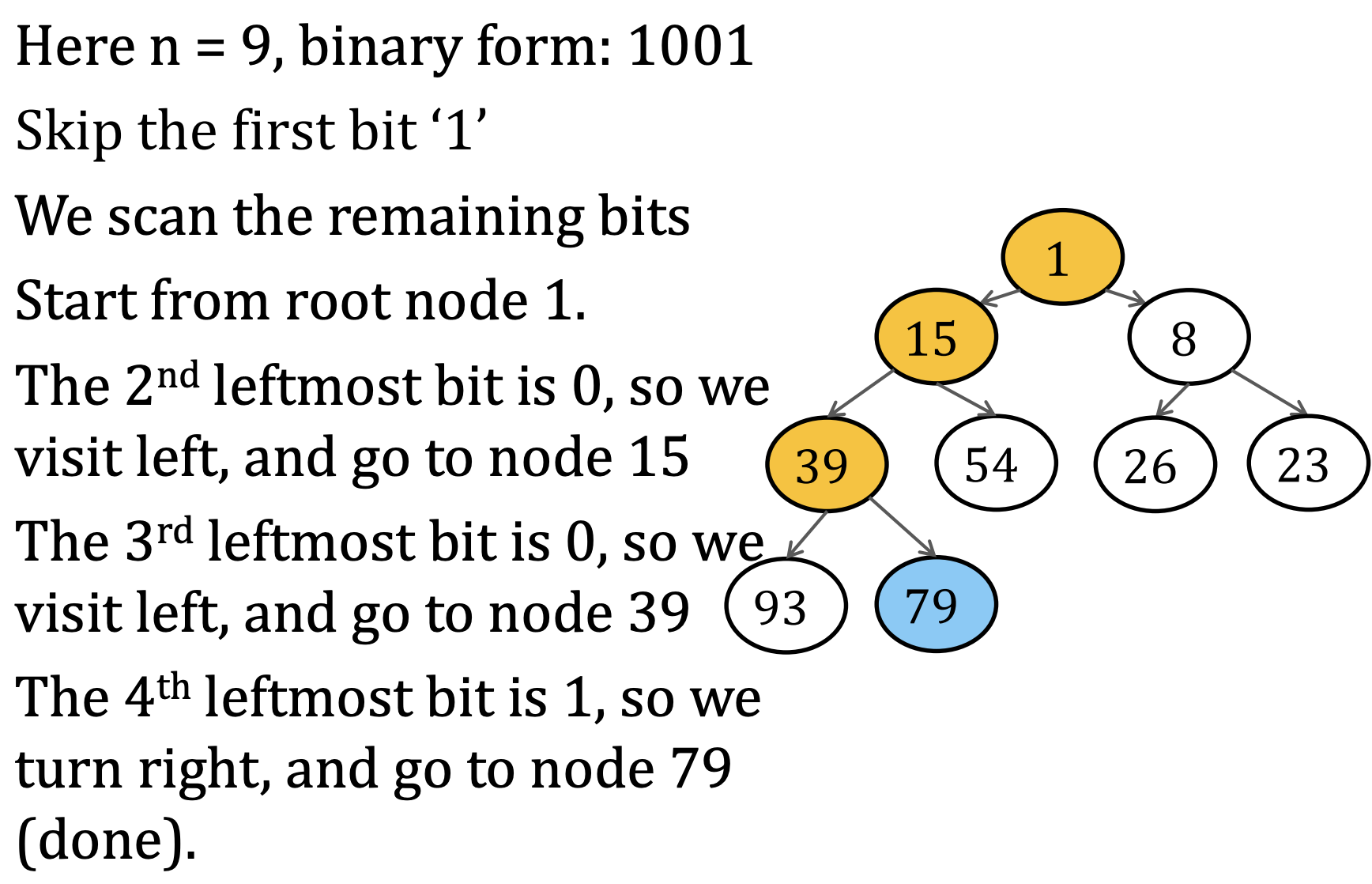
Write the value n in binary form. We can do that in O(log n) time.

Skip the most significant bit. We will scan the remaining bits from left to right, start from root,

If the bit is 0, we go to the left child of the current node

Otherwise, go to right child

Binary Heaps in Dynamic Arrays

Lemma: Suppose that node u of T is stored at A[i]. Then, the left child of u is stored at A[2i], and the right child at A[2i+1].

Corollary: Suppose that node u of T is stored at A[i]. Then, the parent of u is stored at A[ i/2 ].

Lemma: the rightmost leaf node at the bottom level is stored at A[n].

O(n) time to build min-heap

Root fix:

From i=n down to i=1:

swap A[i] and the less child of it.

Proof:

假设目标堆是一个满堆，即第 k 层节点数为 2ᵏ。输入数组规模为 n, 堆的高度为 h, 那么 n 与 h 之间满足 n=2ʰ⁺¹ - 1，可化为 h=log₂(n+1) - 1。 (层数 k 和高度 h 均从 0 开始，即只有根节点的堆高度为0，空堆高度为 -1)。

建堆过程中每个节点需要一次下滤操作，交换的次数等于该节点到叶节点的深度。那么每一层中所有节点的交换次数为节点个数乘以叶节点到该节点的深度（如第一层的交换次数为 2⁰ · h，第二层的交换次数为 2¹ · (h-1)，如此类推）。从堆顶到最后一层的交换次数 Sn 进行求和：

$$S_n = 2^0 \cdot h + 2^1 \cdot (h - 1) + 2^2 \cdot (h - 2) + \cdots + 2^{h-2} \cdot 2 + 2^{h-1} \cdot 1 + 2^h \cdot 0$$ $$S_n = h + 2^1 \cdot (h - 1) + 2^2 \cdot (h - 2) + \cdots + 2^{h-2} \cdot 2 + 2^{h-1}$$

乘2得

$$2S_n = 2^1 \cdot h + 2^2 \cdot (h - 1) + 2^3 \cdot (h - 2) + \cdots + 2^{h-1} \cdot 2 + 2^h$$

相减得

$$S_n = -h + 2^1 + 2^2 + 2^3 + \cdots + 2^{h-1} + 2^h$$

等比数列求和

$$S_n=-h+\dfrac{2*(1-2^h)}{1-2}$$ $$S_n = 2^{h+1} - (h + 2)$$

在前置条件中已得到堆的节点数 n 与高度 h 满足 条件 $n=2^{h+1} - 1$ 和 $h=log_2(n+1) - 1$，分别代入:

$$S_n = n - log₂(n + 1)=O(n)$$

Binary Search Tree

BST operations

Balanced BST