Digital Logic Chapter 5 part 2 - Synchronous Sequential Logic

Analysis of Sequential Circuits

Ways to describe a digital circuit

logic diagram (逻辑电路图): graphical representation of a digital circuit that uses standard symbols

K-map (卡诺图): graphical representation of a logic function used to simplify Boolean expressions

function table (功能表)(truth table): list of all possible input combinations and the corresponding output values for a given logic function

characteristic equations (特征方程): Describe the behavior of a sequential logic circuit, the next state is defined as a function of the inputs and the present state

excitation/input equation (激励方程): Defines the part of the circuit that generates the inputs to sequential logic circuit

state table (状态表): tabular representation of a sequential logic circuit that shows the current state, input, next state, and output for all possible input combinations

state equation (次态方程): defines the next state of a sequential logic circuit based on the current state and input values

state diagram (状态图): graphical representation of a sequential logic circuit that shows the states, transitions, and input-output relationships

Analysis Procedure of Clocked Sequential Circuits

Steps:

1. Derive excitation/input equations for FF inputs
2. Derive state and output equations
   Substitute the excitation equations into the flip-flop characteristic equations to obtain next state equations.
   Determine the output equations according current state and input
3. Generate state and output tables
4. Generate state diagram

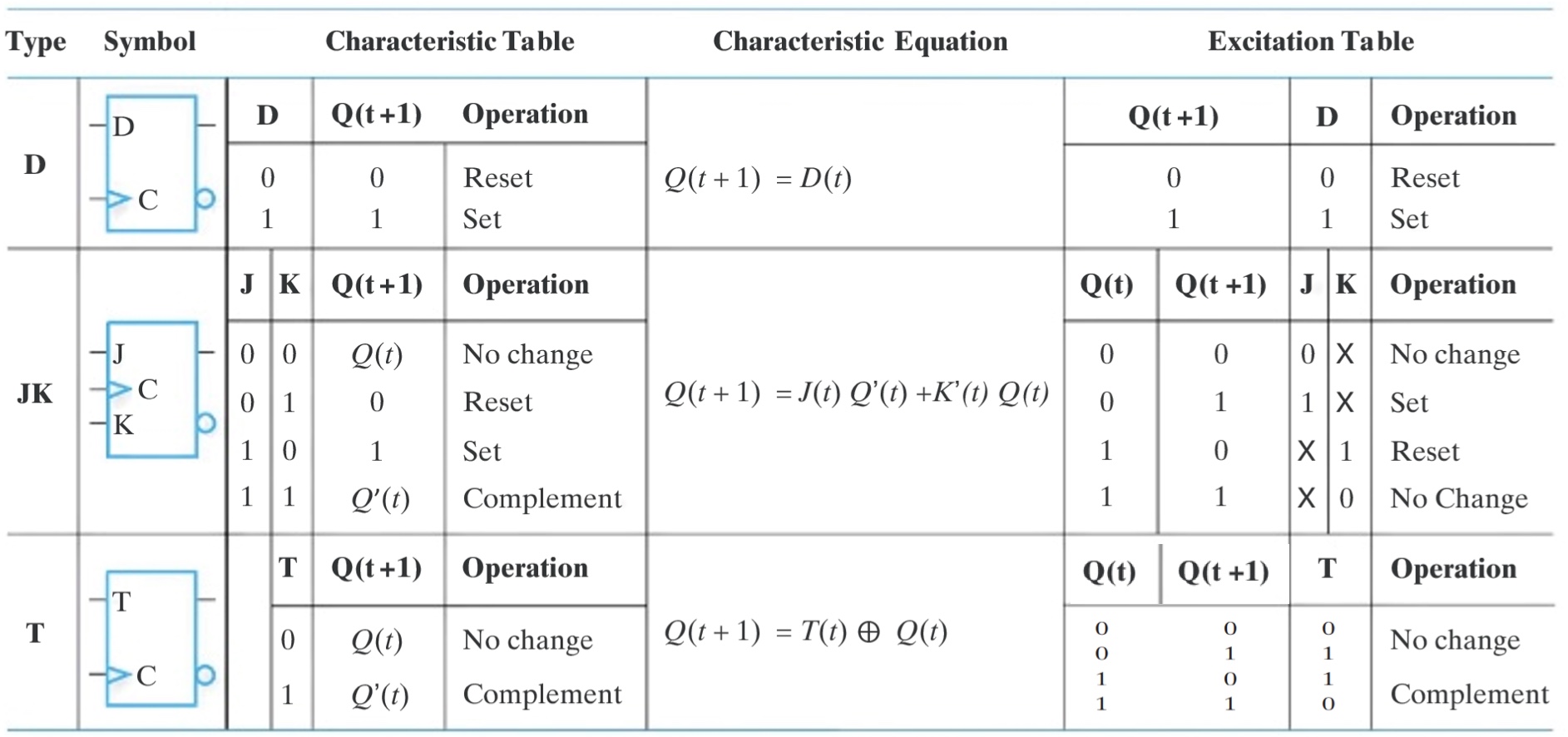
Important: FF’s Characteristic equation:
DFF $Q(t+1) = D(t)$
JKFF $Q(t+1) = J(t)Q(t)’ + K(t)’Q(t)$
TFF $Q(t+1) = T(t)’Q(t) + T(t)Q(t)’$

Example 1 using DFF $Q(t+1) = D(t)$:

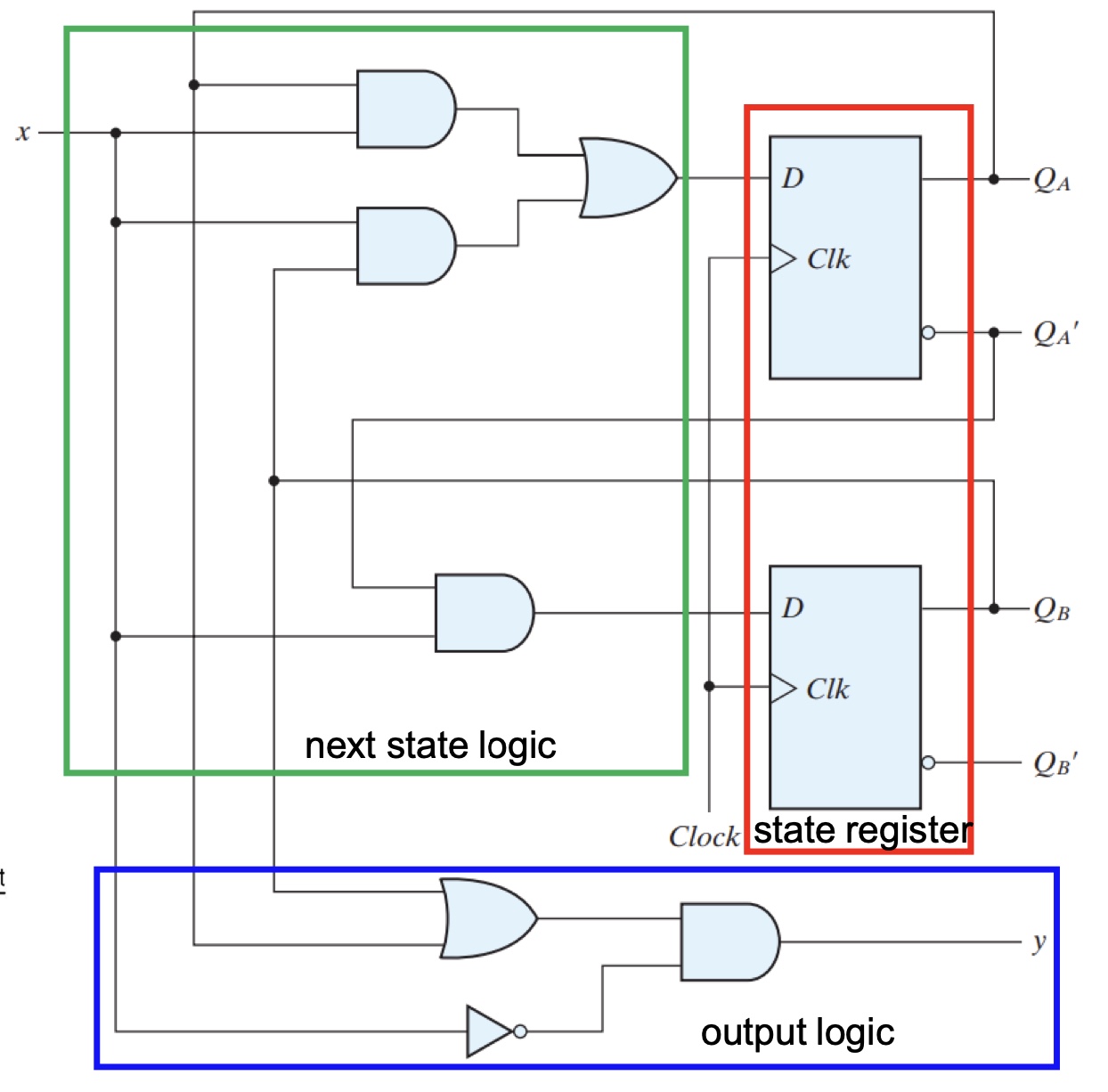
1. Derive excitation/input equations for FF inputs
   $D_A = Q_Ax + Q_Bx$
   $D_B = Q_A’x$
2. State equation
   $Q_A(t+1) = D_A(t)=Q_Ax + Q_Bx$
   $Q_B(t+1) = D_B(t) = Q_A’(t)x(t)$
3. Output equation
   $y(t) = (Q_A(t) + Q_B(t))x’(t)$
   All signals are labeled by t, thus $y = (Q_A + Q_B)x’$
4. Generate state and output tables

Present state	Present state	Input	Next state	Next state	Output
$Q_A$	$Q_B$	$x$	$Q_{Anext}$	$Q_{Bnext}$	$y$
0	0	0	0	0	0
0	0	1	0	1	0
0	1	0	0	0	1
0	1	1	1	1	0
1	0	0	0	0	1
1	0	1	1	0	0
1	1	0	0	0	1
1	1	1	1	0	0

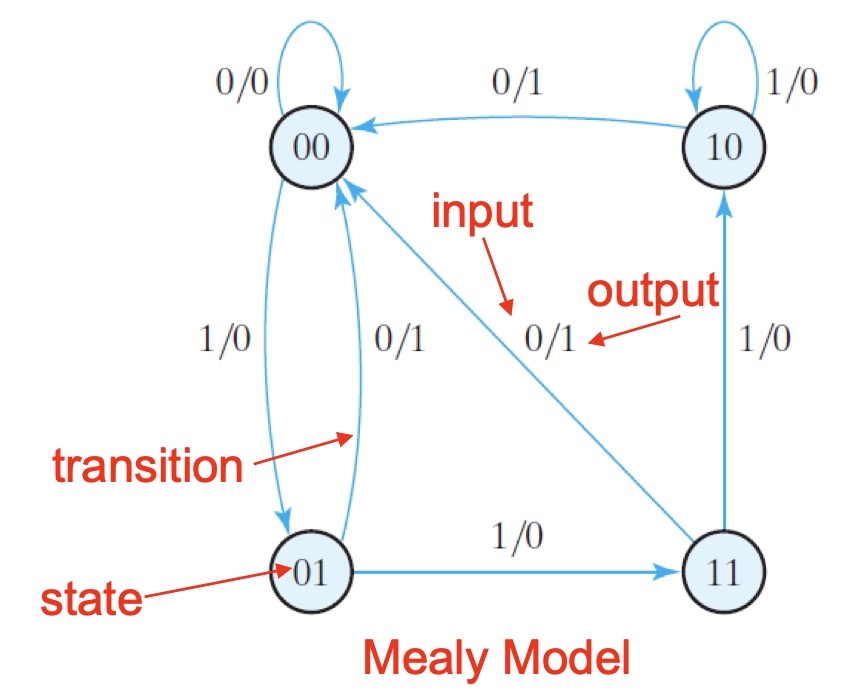
1. Generate state diagram

   

Example 2 using JKFF $Q(t+1) = J(t)Q(t)’ + K(t)’Q(t)$:

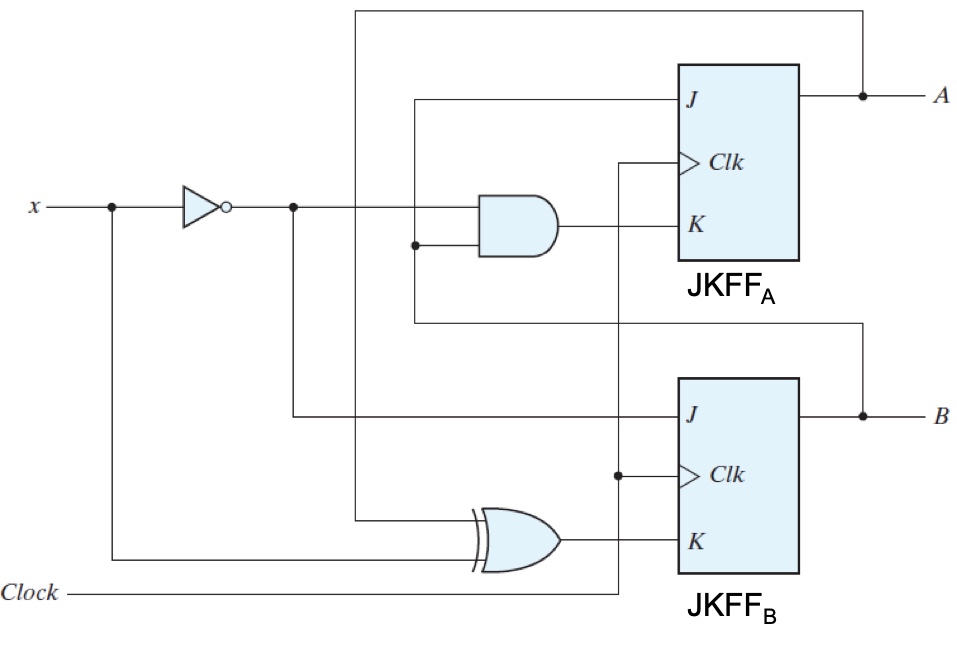
1. Derive excitation/input equations for FF inputs
   $J_A = B$
   $K_A= Bx’$
   $J_B=x’$
   $K_B=A \oplus x$

2. State equation
   $A(t+1) = J_AA’ + K_A’A= BA’ + (Bx’)’A$
   $B(t+1) = J_BB’ + K’_BB=B’x’ +(A \oplus x)’B $

3. No extra output equations

4. Generate state and output tables

Present state	Present state	Input	Next state	Next state	FF inputs	FF inputs	FF inputs	FF inputs
$A$	$B$	$x$	$A_{next}$	$B_{next}$	$J_A$	$K_A$	$J_B$	$K_B$
0	0	0	0	1	0	0	1	0
0	0	1	0	0	0	0	0	1
0	1	0	1	1	1	1	1	0
0	1	1	1	0	1	0	0	1
1	0	0	1	1	0	0	1	1
1	0	1	1	0	0	0	0	0
1	1	0	0	0	1	1	1	1
1	1	1	1	1	1	0	0	0

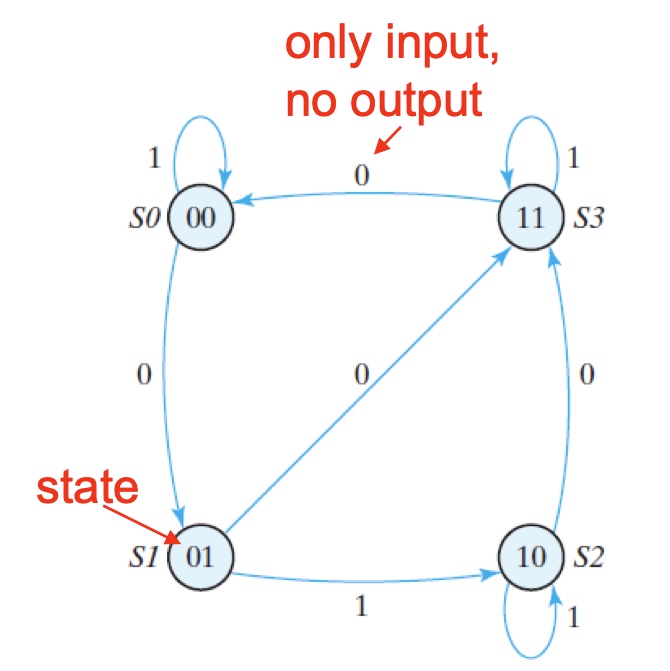
1. Generate state diagram
   

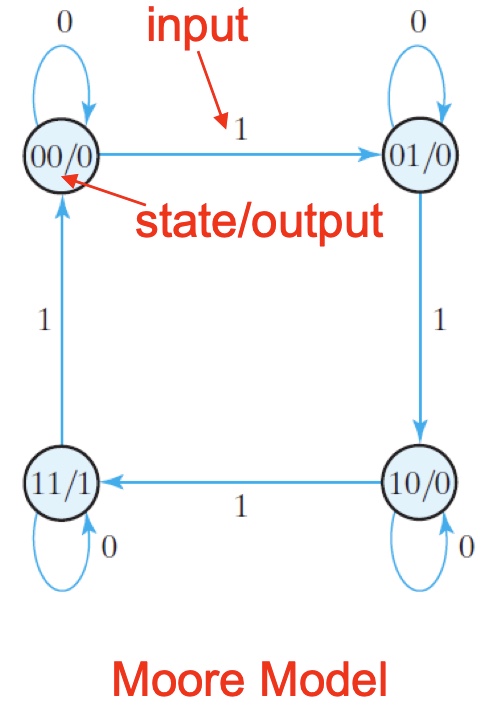
Example 3 using TFF $Q(t+1) = T(t)’Q(t) + T(t)Q(t)’$:

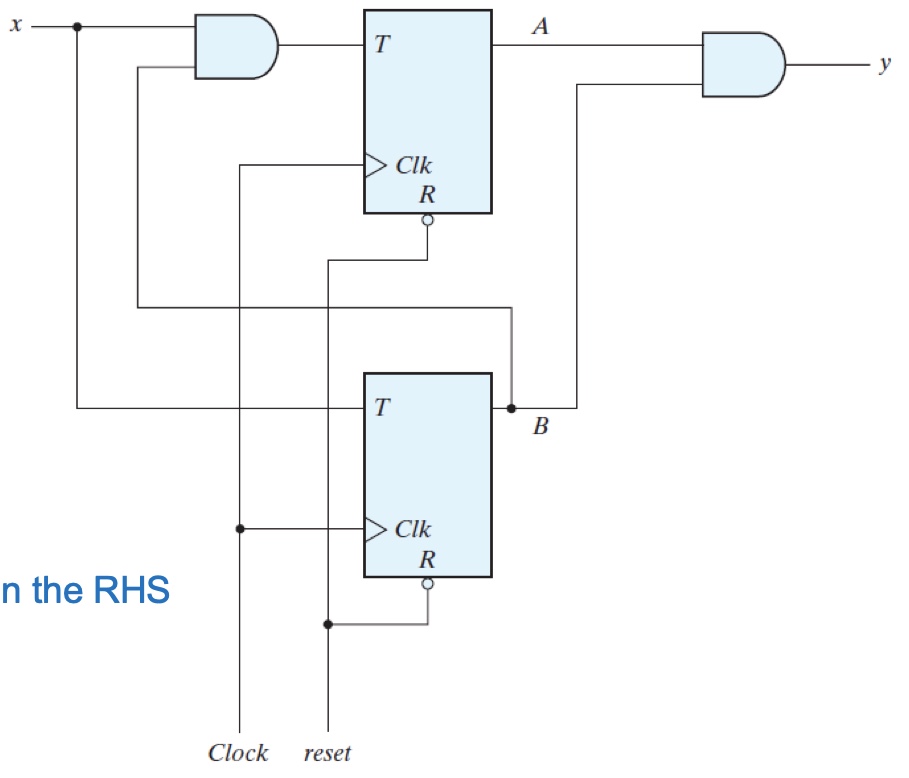
1. Derive excitation/input equations for FF inputs
   $T_A = Bx$
   $T_B = x$

2. State equation
   $A(t+1) = T_A \oplus Q_A = (Bx) \oplus A$
   $B(t+1)=T_B \oplus Q_B = x \oplus B$

3. Output equation
   $y = AB$

4. Generate state and output tables

Present state	Present state	Input	Next state	Next state	Output
$A$	$B$	$x$	$A_{next}$	$B_{next}$	$y$
0	0	0	0	0	0
0	0	1	0	1	0
0	1	0	0	1	0
0	1	1	1	0	0
1	0	0	1	0	0
1	0	1	1	1	0
1	1	0	1	1	1
1	1	1	0	0	1

1. Generate state diagram
   

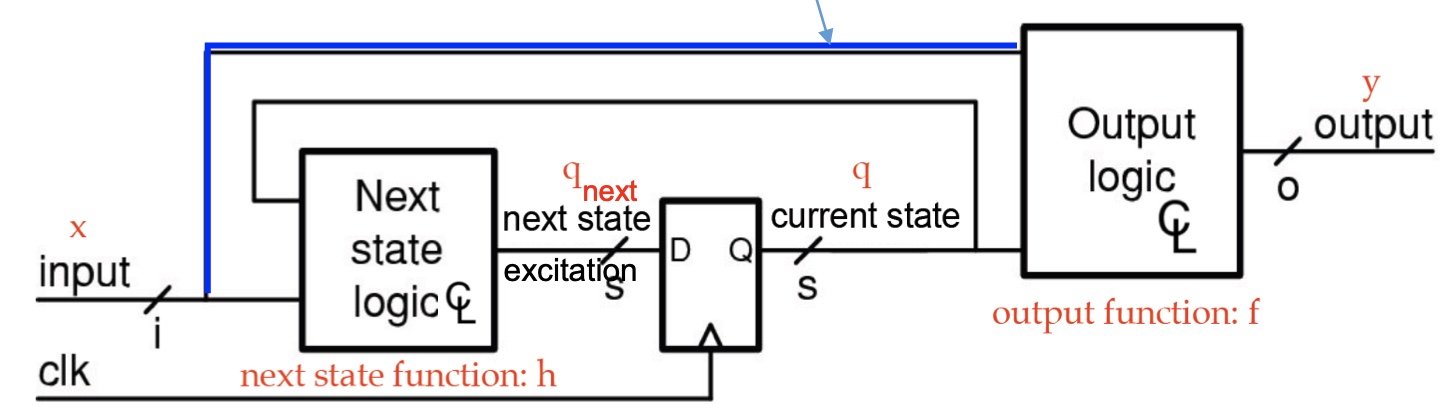
Finite State Machine

A synchronous sequential circuit can be modeled by FSM.

State register $𝑞(t+1) = 𝑞_{next}(t)$
Stores current state
Loads next state at clock edge

Combinational logic
Computes next state (next state logic $h: x × 𝑞 → 𝑞_{𝑛𝑒𝑥𝑡}$ )
Computes outputs
output logic $f: x × 𝑞 → 𝑦$ (Mealy machine, with blue line)
or $f: 𝑞 → 𝑦$ (Moore machine, without blue line)

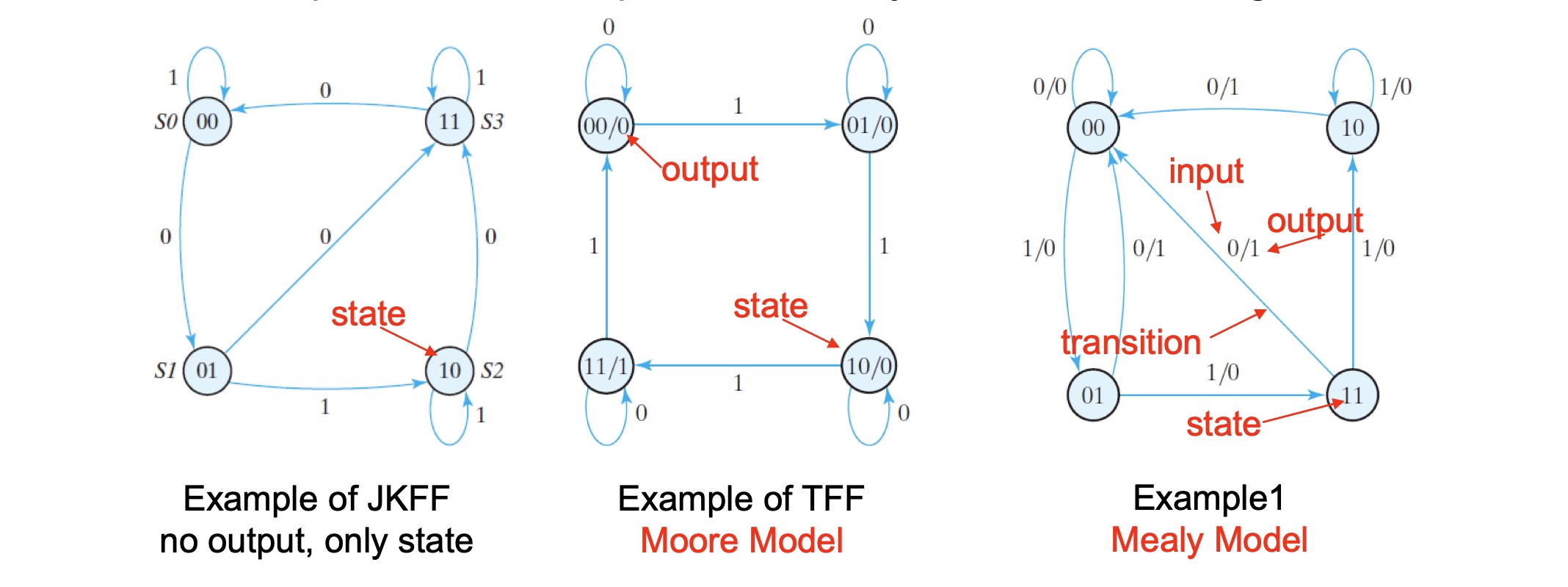
Two types of finite state machines differ in output logic:
Moore FSM: outputs depend only on current state
Mealy FSM: outputs depend on current state and inputs, to synchronize a Mealy circuit, the inputs must be synchronized with the clock and the outputs must be sampled immediately before the clock edge

State Minimization & Encoding

State minimization

Reductions on the number of flip-flops (states) and the number of gates.
For an FSM with m states, we need $log_2m$ FFs.

Reduction steps

1. Find rows in the state table that have identical next state and output entries. They correspond to equivalent states. If there are no equivalent states, stop.
2. When 2 states are equivalent, one of them can be removed. Update the entries of the remaining table to cancel the removed state. Go to 1.

Example: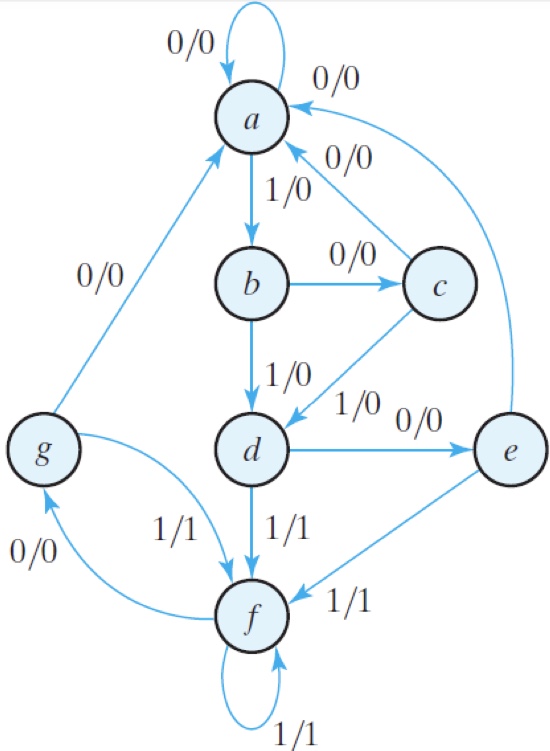
$\longrightarrow$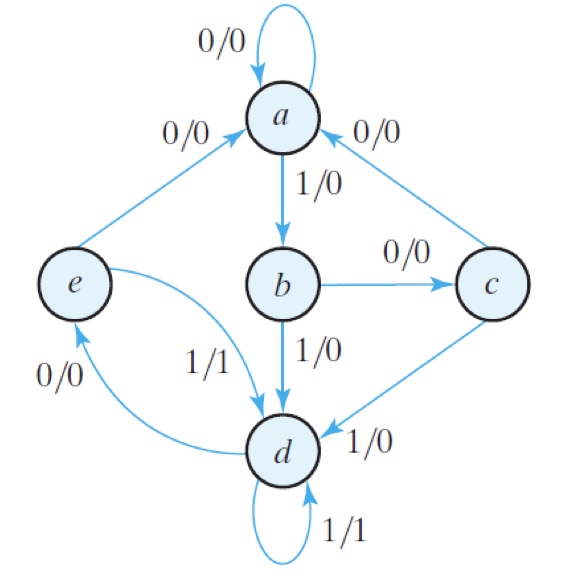

Start table:

Present state	Next state	Next state	Output	Output
	$x=0$	$x=1$	$x=0$	$x=1$
a	a	b	0	0
b	c	d	0	0
c	a	d	0	0
d	e	f	0	1
e	a	f	0	1
f	g	f	0	1
g	a	f	0	1

1st turn: $e \equiv g$

Present state	Next state	Next state	Output	Output
	$x=0$	$x=1$	$x=0$	$x=1$
a	a	b	0	0
b	c	d	0	0
c	a	d	0	0
d	e	f	0	1
e	a	f	0	1
f	g e	f	0	1

2nd turn: $d \equiv f$

Present state	Next state	Next state	Output	Output
	$x=0$	$x=1$	$x=0$	$x=1$
a	a	b	0	0
b	c	d	0	0
c	a	d	0	0
d	e	f d	0	1
e	a	f d	0	1

Encoding(assign binary state to the states)

Different state encodings (assignments) result in different circuits for the intended FSM.
There is no easy state-encoding procedure that guarantees a minimal-cost or minimum-delay combinational circuits
Exploration of all possibilities are impossible.
Heuristic are often used.
Binary counting
Minimum-bit change
One-hot encoding

Design of Sequential Circuits

Design Procedure of Sequential Circuits

1. Specification: design description or timing diagram
2. Formulation: develop state diagram
3. Generate state and output tables
4. Minimize States if necessary
5. Assign binary values to the state (encoding)
6. Derive state and output equations
7. Choose memory elements (DFFs, JKFFs, TFFs)
8. Derive simplified excitation/input equations and output equations
9. Draw logic schematic

Choice of Memory Elements

Given the state transition table, we wish to find the FF input conditions that will cause the required transition.
A tool for such a purpose is the excitation table, which can be derived from the characteristic table/equation.
D FFs are good for applications requiring data transfer (shift registers).
T FFs are good for those involving complementation (binary counters).
Many digital systems are constructed entirely with JK FFs because they are the most versatile available.

FF’s Excitation Table

Design Example: Design with DFF: A Sequence Detector

1. Detect three consecutive 1’s in a string of bits (using Moore machine, overlapping)
   If detected, output=1; otherwise output=0

2. State diagram
   

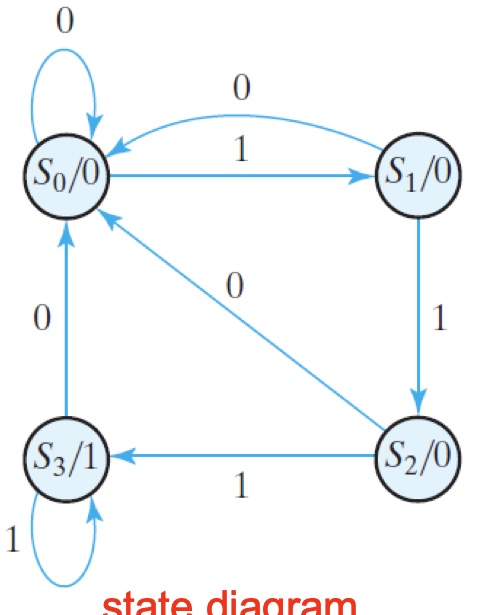
3. State and output table

Present state	Next state	Next state	Output	Output
$S(AB)$	$x=0$	$x=1$	$x=0$	$x=1$
$S_0 (00)$	$S_0$	$S_1$	0	0
$S_1(01)$	$S_0$	$S_2$	0	0
$S_2(10)$	$S_0$	$S_3$	0	0
$S_3(11)$	$S_0$	$S_3$	1	1

1. No need for simplification

2. State assignment in 3

3. Derive state and output equations

$A(t)$	$B(t)$	$x$	$A(t+1)$	$B(t+1)$	$y$
0	0	0	0	0	0
0	0	1	0	1	0
0	1	0	0	0	0
0	1	1	1	0	0
1	0	0	0	0	0
1	0	1	1	1	0
1	1	0	0	0	1
1	1	1	1	1	1

$A(t+1)=D_A(A(t),B(t),x)=\Sigma(3,5,7)$
$B(t+1)=D_B(A(t),B(t),x)=\Sigma(1,5,7)$
$y(A,B,x)=\Sigma(6,7)$

1. Choose DFFs
   2 bits encoding leads to 2 DFFs.
   $A(t+1) =D_A(t)$
   $B(t+1)=D_B(t)$

2. Derive simplified excitation/input equations and output equations
   
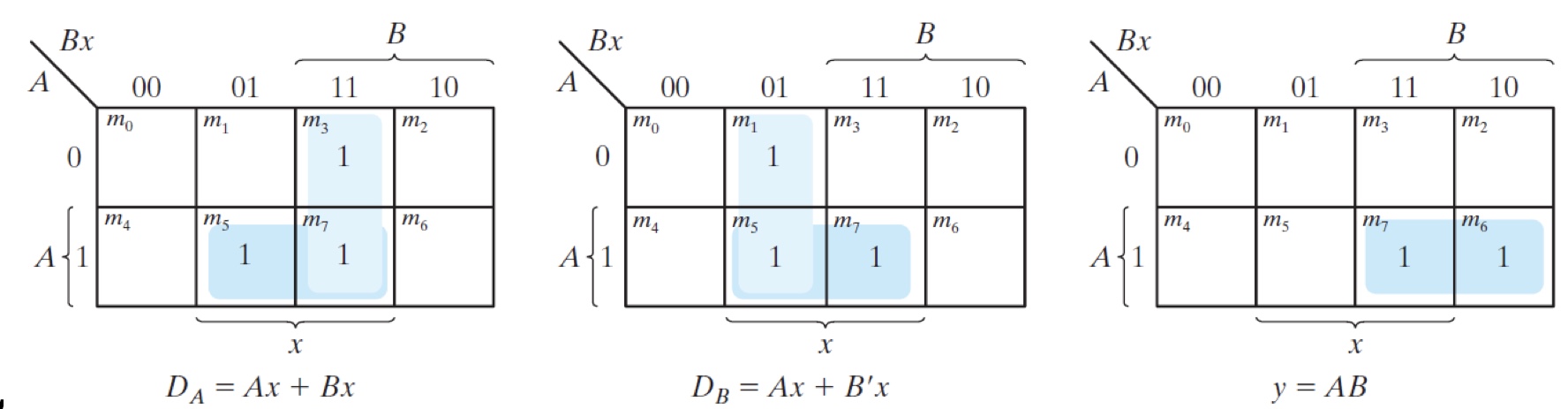
   $D_A=Ax+Bx$
   $D_B=Ax+B’x$
   $y=AB$

3. Logic schematic(Omitted)