Discrete Math Chapter 6 - Induction and Recursion

Mathematical Induction

Principle of Mathematical Induction

Let $P(n)$ be a predicate. i.e., $P(n)$ is either true or false when $n$ is a specific number.
Principle of Mathematical Induction: To prove that $P(n)$ is true for all positive integers $n \in Z^+$, we complete 2 steps:
Basic step: prove $P(1)$ is true;
Inductive step: prove $\forall k \in Z^+,P(k) \rightarrow P(k+1)$ is true.
(“$P(k)$ is ture” is called the inductive hypothesis (IH)归纳假设)

Why this principle is valid?
Proof by contradiction: Assume $P(n)$ is false for some integer $n ≥ 1$, then the set $S$ of all positive integer n such that $P(n)$ is false is not empty. Let m be the smallest integer in $S$.
Why such m exists?
We have $m ≥ 2$ as $P(1)$ is true. However, since $P(m – 1)$ is true and $P(m – 1) → P(m)$ is true, $P(m)$ must be true, contradiction!

Well-Ordering Principle

Well-Ordering Principle: every nonempty subset of $Z^+$ has a least/minimum element $\longrightarrow$ this is an axiom.
This principle is equivalent to mathematical induction.

This also means mathematical induction can be generalized from $Z^+$ to any well-ordered set $S$, e.g., $N, {n \in Z | n \geq b}$, etc.

Another Form of Induction

Consider another form of mathematical induction as follows:
First suppose that we have a proof that $P(1)$ is true.
Next suppose that we have a proof that $∀k ≥ 1, P(1) ∧ P(2) ∧ ··· ∧ P(k) → P(k + 1)$
Then, $P(1) → P(2) P(1) ∧ P(2) → P(3) P(1) ∧ P(2) ∧ P(3) → P(4) …$
Iterating gives us a proof of $P(n)$ for all $n$.

Strong Induction

Second principle of mathematical induction: To prove that $P(n)$ is true for all positive integers $n$, we complete two steps:
Basis step: prove $P(1)$ is true
Inductive step: prove $∀k ∈ Z+ , P(1) ∧ ··· ∧ P(k) → P(k + 1)$ is true
(here “$P(1) ∧ P(2) ∧ ··· ∧ P(k)$ is true” is the inductive hypothesis (IH))

This is called strong induction or complete induction, while the previous principle is called weak or incomplete induction.
In practice, strong induction is often easier to apply than its weak form, because the inductive hypothesis is stronger.
However, these two forms of induction are actually equivalent.

Core idea

The assumption “$P(k)$ is true” OR “$P(1) ∧ P(2) ∧ ··· ∧ P(k)$ is true” is called the inductive hypothesis (IH).
IH is used as premises to prove the conclusion “$P(k + 1)$ is true” .

Recursion

Definition

Recursion: a method of solving a computational problem where its solution depends on solutions to smaller instances of the same problem.
Recursive computer programs or algorithms often lead to inductive analysis.
A classical example of recursion is the Towers of Hanoi puzzle.

Towers of Hanoi Puzzle

Problem: Find an efficient way to move all of the disks from one peg to another, using only legal moves.
Consider 3 pegs and $n$ disks of different sizes.
A legal move takes a disk from one peg and moves it onto another peg so that it is not on top of a smaller disk.

Solution

Solution by recursion: very similar to mathematical induction
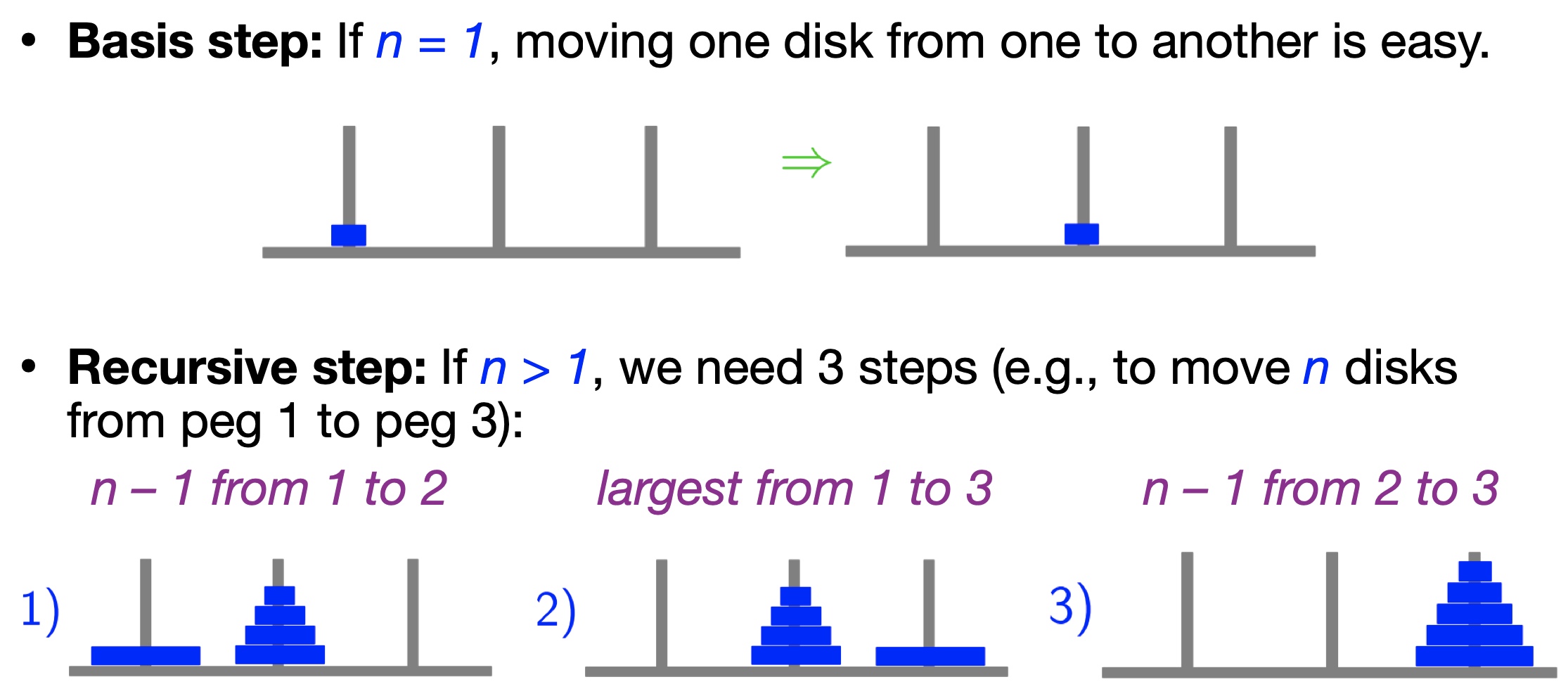
Basis step: If n = 1, moving one disk from one to another is easy.
Recursive step: If n > 1, we need 3 steps (e.g., to move n disks from peg 1 to peg 3):
1)n – 1 from 1 to 2
2)largest from 1 to 3
3)n – 1 from 2 to 3

public class Hanoi {
    public void move(int n, char a, char b, char c) { //move n disks from peg a to peg c using peg b
        if (n == 1) {
            System.out.println("plate" + n + " from " + a + " to " + c);
        } else {
            move(n - 1, a, c, b); //move n-1 disks from a to b using c
            System.out.println("plate" + n + " from " + a + " to " + c); //move the largest disk from a to c
            move(n - 1, b, a, c); //move n-1 disks from b to c using a
        }
    }
}

Proof of correctness (of solution) by induction:

Let $P(n)$ be the predicate that the solution is correct for $n$.
Basis step: $P(1)$ is obviously true, i.e., the solution is correct when there is only one disk.
Inductive step: From the inductive hypothesis, i.e., $P(k)$ is true for an arbitrary positive integer $k$, we need to show that $P(k + 1)$ is true. That is, if our solution works for $k$ disks, then we can build a correct solution for $k + 1$ disks, which is true by the recursive step:

Running Time

Let $M(n)$ be the number of disk moves.
Basic step: If $n=1$, moving one time only, $M(1)=1$ obviously.
Recursive step: If $n>1$, we need three steps, $M(n) = 2M(n-1)+1$ for $n>1$
We can guess $M(n)=2^n-1$, proof using mathematical induction, thus omitted.

Recurrence Relations

A recurrence relation or recurrence for a function defined on the set of $integers ≥ b$ tells us how to compute the $nth$ value from some or all of the first $n – 1$ values.
To completely specify a function defined by a recurrence, we have to also give the initial condition(s) (as known as the base case(s)) for the recurrence.
Example: running time for Towers of Hanoi

$$M(n)= \begin{cases} 1& \text{$n=1$}\\ 2M(n-1)+1& \text{$otherwise$} \end{cases}$$

Iterating a Recurrence

Let $T(n) = rT(n − 1) + a$, where $r$ and $a$ are constants.
Find a recurrence relation that expresses
$T(n)$ in terms of $T(n − 2)$
$T(n)$ in terms of $T(n − 3)$
$T(n)$ in terms of $T(n − 4)$
…
Can we generalize this to find a closed-form solution to $T(n)$?
Note that $T(n) = rT(n − 1) + a$ implies that $\forall (n – i) > 0$: $T(n − i) = rT((n − i) − 1)) + a$
$T(n)=rT(n-1)+a=r^2T(n-2)+ra+a=r^3T(n-3)+r^2a+ra+a=…$
Guess: $T(n)=r^nT(0)+a\sum^{n-1}_{i=0}r^i$
The technique we used to guess the closed formula of $T(n)$ is called iteration, because we iteratively use the recurrence.
The approach we just used is called backward substitution, because we began with $T(n)$ and iterated to express it in terms of falling terms of the sequence until we found it in terms of $T(0)$.

Closed Formula of Recurrences

Theorem: If $T(n) = rT(n − 1) + a, T(0) = b$, and $r ≠ 1$, then for all non-negative integers $n$, we have:

​ $T(n)=r^nb+a\dfrac{1-r^n}{1-r}$

Proof by induction:
Basis step: The formula is true for n = 0: $T(0)=r^0b+a\dfrac{1-r^0}{1-r}=b$
Inductive step:$T(n) = rT(n-1)+a=r(r^{n-1}b+a\dfrac{1-r^{n-1}}{1-r})=r^nb+\dfrac{ar-ar^n+a+ar}{1-r}=r^nb+a\dfrac{1-r^n}{1-r}$

First Order Linear Recurrences

Theorem: For any constants $a$ and $r ≠ 0$, and any function $g$ defined on positive integers, the solution to the recurrence

$$T(n)= \begin{cases} a& \text{$n=0$}\\ rT(n-1)+g(n)& \text{$n>0$} \end{cases}$$

We have $T(n)=r^na+\sum^{n}_{i=1}r^{n-i}g(i)$

A recurrence relation of the form $T(n) = f(n)T(n − 1) + g(n)$ is called a first-order linear recurrence.
First order: $T(n)$ depends upon going back one step, i.e., $T(n −1)$,
e.g., $T(n) = T(n − 1) + 2T(n − 2)$ is a second-order recurrence.
Linear: the $T(n − 1)$ only appears to the first power
e.g., $T(n) = (T(n − 1))2 + 3$ is a non-linear first-order recurrence.

Divide-and-Conquer Recurrences

Divide and conquer (D&C): recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly; the solutions to the sub-problems are then combined to give a solution to the original problem.

Divide-and-conquer recurrence relations are usually of the form: $T(n)= \begin{cases} \text{something given}& \text{if $n\le n_0$}\\ r\cdot T(\dfrac{n}{m})+g(n)& \text{if $n> n_0$} \end{cases}$

Example: Binary Search

Problem: Someone has chosen an integer x between 1 and n. We need to find this secret
We only need to ask two types of questions:
Is x greater than k?
Is x equal to k?
Strategy: We first always ask greater than questions, at each step halving our search range, until the range contains only one number, then we ask a final equal to question.

D&C: Each guess reduces the size of the problem to only half as big, then we can (recursively) conquer this smaller problem.
When n is a power of 2, the number of comparisons T(n) in a binary search on {1, 2, …, n} satisfie

$$T(n)= \begin{cases} 1& \text{$n=1$}\\ T(\dfrac{n}{2})+1& \text{$n\geq2$} \end{cases}$$

Proof of correctness (by strong induction) of the running time:
Basis step ($n = 1$): only one “equal to” comparison is needed
Inductive step ($n ≥ 2$): one “great than” comparison + time to perform binary search on the remaining $n/2$ term

Solve by iteration:
$T(n)=T(\dfrac{n}{2})+1=T(\dfrac{n}{2^2})+2=T(\dfrac{n}{2^i})+i$
Note that this terminates when $i=log_2n$
$T(n)=T(\dfrac{n}{2^{log_2n}})+log_2n=1+log_2n$

Example 1: $T(n)= \begin{cases} 1& \text{$n=1$}\\ 2T(\dfrac{n}{2})+n& \text{$n\geq2$} \end{cases}$

This corresponds to solving a problem of size n, by either
(i) solving 2 subproblems of size $n/2$;
(ii) doing $n$ units of additional work or using $T(1)$ work for the case of $n = 1$.
this is exactly how Merge Sort (from an algorithm course) works.

Solve by iteration:
$T(n)=2T(\dfrac{n}{2})+n=4T(\dfrac{n}{4})+2n=…=2^iT(\dfrac{n}{2^i})+in$
Note that this terminates when $i=log_2n$
$T(n)=2^{log_2n}T(\dfrac{n}{2^{log_2n}})+n\cdot log_2n=nT(1)+nlog_2n$

Example 2: $T(n)= \begin{cases} 1& \text{$n=1$}\\ T(\dfrac{n}{2})+n& \text{$n\geq2$} \end{cases}$

This corresponds to solving a problem of size n, by either
(i) solving 1 subproblem of size $n/2$;
(ii) doing $n$ units of additional work or using $T(1)$ work for the case of $n = 1$.

Solve by iteration:
$T(n)=T(\dfrac{n}{2})+n=T(\dfrac{n}{2^2})+\dfrac{n}{2}+n=T(\dfrac{n}{2^3})+\dfrac{n}{2^2}+\dfrac{n}{2}+n=…=T(\dfrac{n}{2^i})+\dfrac{n}{2^{i-1}}+…+\dfrac{n}{2^2}+\dfrac{n}{2}+n$
Note that this teminates when $i=log_2n$
$T(n)=T(\dfrac{n}{2^{log_2n}})+\dfrac{n}{2^{log_2n-1}}+…+\dfrac{n}{2^2}+\dfrac{n}{2}+n=1+2+2^2+2^3+…+\dfrac{n}{2^2}+\dfrac{n}{2}+n=2n-1$ //geometric series’ sum

Example 3:$T(n)= \begin{cases} 1& \text{$n=1$}\\ 4T(\dfrac{n}{2})+n& \text{$n\geq2$} \end{cases}$

This corresponds to solving a problem of size n, by either
(i) solving 4 subproblem of size $n/2$;
(ii) doing $n$ units of additional work or using $T(1)$ work for the case of $n = 1$.

Solve by iteration:
$T(n)= 4T(\dfrac{n}{2})+n=4^2T(\dfrac{n}{2^2})+\dfrac{4}{2}n+n=4^3T(\dfrac{n}{2^3})+\dfrac{4^2}{2^2}n+\dfrac{4}{2}n+n=…=4^iT(\dfrac{n}{2^i})+\dfrac{4^{i-1}}{2^{i-1}}n+…+\dfrac{4}{2}n+n$
Note that this teminates when $i=log_2n$

$$T(n)=4^{log_2n}T(\dfrac{n}{2^{log_2n}})+\dfrac{4^{log_2n-1}}{2^{log_2n-1}}n+...+\dfrac{4}{2}n+n=n^2+(\dfrac{n^2/4}{n/2}n)+(\dfrac{n^2/4^2}{n/2^2}n)...+2n+n=n^2+\dfrac{1}{2}n^2+\dfrac{1}{2^2}n^2+...+\dfrac{4}{2}n+n$$

Part 1 is $4^{log_2n}T(\dfrac{n}{2^{log_2n}})=n^2$

Part 2 is $\dfrac{4^{log_2n-1}}{2^{log_2n-1}}n+…+\dfrac{4}{2}n+n$, each item can be written as $2^kn$, which is a geometric series of common ratio 2.

Thus, $\sum^{k-1}_{i=0}2^i=2^k-1=(n-1)$

So, Part 2 = $(n-1)n$

$$T(n)= 2n^2-1$$

Master Theorem

Compare the iteration for the following recurrences ($T(1) = 1$):
$T(n) = T(n / 2) + n$ $T(n) = 2n – 1 = Θ(n)$
$T(n) = 2T(n / 2) + n$ $T(n) = n + n log_2 n = Θ(n log n)$
$T(n) = 4T(n / 2) + n $ $T(n) = 2n2 – n = Θ(n2)$
All three recurrences iterate $log_2n$ times. The size of subproblem in next iteration is half the size in the preceding iteration level.

Theorem: Consider a recurrence relation $T(n) = aT(n / 2) + n$ whenever $n = 2^k$, where $a ≥ 1$ and $T(1) = Θ(1)$.
Then we have the following big Θ bounds on the solution:
If $1 ≤ a < 2$, then $T(n) = Θ(n)$.
If $a = 2$, then $T(n) = Θ(n log n)$.
If $a > 2$, then $T(n) = Θ(n^{log2a}).$

Master Theorem: For a recurrence relation $T(n) = aT(n / b) + cn^d$ whenever $n = b^k$, where $a ≥ 1$, $c > 0$, $d ≥ 0$, integer $b ≥ 2$, and $T(1) = Θ(1)$, we have the following big Θ bounds on the solution:
If $1 ≤ a < b^d$, then $T(n) = Θ(n^d)$.
If $a = b^d$, then $T(n) = Θ(n^d log n)$.
If $a > b^d$, then $T(n) = Θ(n^{log_ba})$.

Exercises

1. Show that $1 + 2 + ··· + n = n(n + 1)/2$ for any positive integer n.

Proof by mathematical induction:
Let P(n) be the predicate that the sum of the first n positive integers is equal to n(n + 1)/2.
Basis step: $P(1)$ is true, because $1 = 1(1 + 1)/2$.
Inductive step: From the inductive hypothesis, i.e., $P(k)$ is true for an arbitrary positive integer $k$, we need to show that $P(k + 1)$ is true, i.e., $1 + 2 + ··· + k + 1 = (k + 1)((k + 1) + 1)/2$.
$1 + 2 + ··· + k + (k + 1) = k(k + 1)/2 + k + 1 = (k(k + 1) + 2(k + 1))/2 = (k + 1)(k + 2)/2 = (k + 1)((k + 1) + 1)/2$
By mathematical induction, we know that $P(n)$ is true for all positive integers $n$. That is, we have proven that $1 + 2 + ··· + n = n(n + 1)/2$ holds for all positive integers $n$.

2. Prove that for any integer $n ≥ 2, 2^{n+1} ≥ n^2 + 3$ .

Proof by mathematical induction:
Let $P(n)$ be the predicate that $\forall n ≥ 2, 2^{n+1} ≥ n^2 + 3$
Basic step: $P(1)$ is true, because $2^{1+1}=4 \geq 1^2+3=4$
Inductive step: From the inductive hypothesis, i.e., $P(k)$ is true for an arbitrary positive integer $k$, we need to show that $P(k + 1)$ is true, i.e., $2^{(k+1)+1} \geq (k+1)^2+3$
$2^{(k+1)+1} \geq 2 \cdot2^{(k+1)} \geq 2(k^2+3) = 2k^2+6=(k+1)^2+(k-1)^2+4\geq (k+1)^2+3$
By mathematical induction, $P(n)$ is true for all integers $n ≥ 2$.

3. Prove: Every positive integer is a power of a prime or the product of powers of primes.

Proof by strong induction: $P(n)$: “$n$ is a power of a prime or the product of powers of primes”
Basis step: $P(1)$ is true, as 1 is a power of a prime number, $1 = 2^0$
Inductive step: Inductive hypothesis: $P(m)$ is true for every $m$ that $1 ≤ m ≤ k$, i.e., $m$ is a power of a prime or a product of powers of primes.
If $k + 1$ is a prime power, $P(k + 1)$ is true.
Otherwise, $k + 1$ must be a composite, i.e., a product of two smaller positive integers, each of which is, by the inductive hypothesis, a power of a prime or the product of powers of primes. Therefore, $P(k + 1)$ is true.
Finally, by strong induction, $P(n)$ is true for all positive integers.

4. Solve $T(n) = rT(n − 1) + g(n)$ with $T(0) = a$ and constant $r ≠ 0$.

Hint: write $T(n)$ in terms of $r, n$, $T(0)$ and $g(i)$

$T(n) = rT(n − 1) + g(n)=r(rT(n − 2) + g(n-1))+g(n)=r^2T(n-2)+rg(n-1)+g(n)=…$

We have $T(n)=r^nT(0)+\sum^{n-1}_{i=0}r^{i}g(n-i)$

5. Solve $T(n) = 4T(n − 1) + 2^n (n > 0)$ with $T(0) = 6$

Hint: write $T(n)$ in terms of $4^n$ and $2^n$

$$T(n)=4^n\cdot6+\sum^{n}_{i=1}4^{n-i}2^i=4^n\cdot6+4^n\sum^n_{i=1}4^{-i}\cdot2^i=4^n\cdot6+4^n\sum^n_{i=1}(\frac{1}{2})^i=4^n\cdot6+4^n\cdot(1-\dfrac{1}{2^n})=7\cdot4^n-2^n$$

6.Solve this recurrence by iteration $T(n)= \begin{cases} 1& \text{$n<3$}\\ 3T(\dfrac{n}{3})+n& \text{$n\geq3$} \end{cases}$

This corresponds to solving a problem of size n, by either
(i) solving 3 subproblem of size $n/3$;
(ii) doing $n$ units of additional work or using $T(1)$ work for the case of $n <3$.

$T(n)=3T(\dfrac{n}{3})+n=3^2T(\dfrac{n}{3^2})+2n=…=3^iT(\dfrac{n}{3^i})+in$
Note that this teminates when $i=log_3n$
$T(n)=3^{log_3n}T(\dfrac{n}{3^{log_3n}})+nlog_3n=nT(1)+nlog_3n=n+nlog_3n$